1C. Subspaces

Definition:

A subset $U\subset V$ is called a subspace of $V$ if $U$ is also a vector space with the same additive identity, addition, and scalar multiplication as on $V$.

Think subgroups from Vector Spaces in Abstract Algebra

Conditions:

The following is the easiest way to check whether a subset of a vector space is a subspace: A subset $U$ of $V$ is a subspace if and only iff $U$ meets three conditions:

1. Additive identity. $0\in U$
2. Closed under addition. $u+w\in U\forall u,w\in U$
3. Closed under scaler multiplication. $\lambda u\in U$ for all $\lambda \in \mathbb{F}$ and $u\in U$

Proof: $\Rightarrow$

1. Suppose $U$ is a subspace of $V$. Then it has the same properties of addition, scaler multiplication, and identity. By this, we know it contains $0$, is closed under addition and it closed under scaler multiplication.

$\Leftarrow$

1. Suppose $U$ is a subset of $V$ where the following are true:
   1. $0\in U$
   2. Additive closure, $u+w\in U$ for all $u,w\in U$
   3. Closed under scaler multiplciation; $\lambda u\in U$ for all $\lambda \in \mathbb{F}$ and $u\in U$
2. Lets use these to prove the axioms required for a vector space:
   1. Additive Commutativity:
      1. Met as $U$ is just a part of $V$
   2. Additive Asociativity:
      1. Met as $U$ is just a part of $V$
   3. Additive Identity:
      1. This is clearly met by condition 1.
   4. Additive Inverse:
      1. Notice for any $u\in U$ we have it so $(-1)u=-u\in U$ as $-1\in \mathbb{F}$.
   5. Scaler Multiplication Asociativity:
      1. Met as $U$ is just a part of $V$
   6. Scaler Multiplication Identity:
      1. You are still a vector space over $\mathbb{F}$ which contains $1$. Thus by condition 3 this holds.
   7. Distributive Properties.
      1. Met as $U$ is just a part of $V$

Exercises:

Lets prove that the following are subspaces.

1.

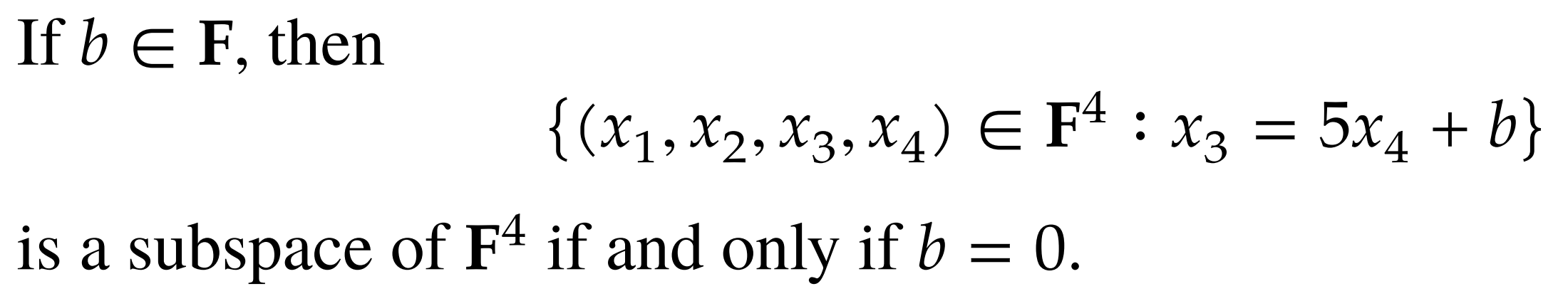Proof: For $b\in \mathbb{F}$, $\{(x_1,x_2,x_3,x_4)\in {\mathbb{F}}^4\mid x_3=5x_4+b\}$ is a subspace of ${\mathbb{F}}^4$ $⟺$ $b=0$. Let $U=\{(x_1,x_2,x_3,x_4)\in {\mathbb{F}}^4\mid x_3=5x_4+b\}$ $\Rightarrow$

1. Assume $\{(x_1,x_2,x_3,x_4)\in {\mathbb{F}}^4\mid x_3=5x_4+b\}$ is a subspace of ${\mathbb{F}}^4$.
2. Then $U$ must contain the $0$ vector; $(0,0,0,0)$
3. This is only possible if $0=5(0)+b$
4. Then, $b=0$ $\Leftarrow$
5. Assume $b=0$
6. By definition $U\subset V$ as it only contains elements in ${\mathbb{F}}^4$
7. $0\in U$:
   1. as we know the $0$ vector is $(0,0,0,0)$. Letting $x_3=x_4=0$
   2. Notice $0=5(0)+0$.
   3. This satisfies the condition for $0\in U$
8. Additive Closure:
   1. Assume any $a,b\in U$
   2. Then we have the following:
      1. $a=(a_1,a_2,5a_4,a_4)$
      2. $b=(b_1,b_2,5b_4,b_4)$
   3. Notice the following: $a+b=(a_1,a_2,5a_4,a_4)+(b_1,b_2,5b_4,b_4)=(a_1+b_1,a_2+b_2,5a_4+5b_4,a_4+b_4)$
   4. Additionally, notice $(a_1+b_1,a_2+b_2,5a_4+5b_4,a_4+b_4)=(a_1+b_1,a_2+b_2,5(a_4+b_4),a_4+b_4)$.
   5. As the third coordinate is the 4th coordinate multiplied by $5$; This meets the conditions for it to be in $U$.
   6. Thus for any $a,b\in U⟹(a+b)\in U$.
9. Closed by Scaler Multiplication:
   1. Let $u\in U$ and $\lambda \in \mathbb{F}$.
   2. With this, we can define $u$ as: $u=(u_1,u_2,5u_4,u_4)$
   3. Now, notice the following: $\lambda u=\lambda (u_1,u_2,5u_4,u_4)=(\lambda u_1,\lambda u_2,\lambda 5u_4,\lambda u_4)=(\lambda u_1,\lambda u_2,5(\lambda u_4),\lambda u_4)$
   4. As the third coordinate is still the 5 times the 4th coordinate, we know $\lambda u\in U$.

2.

Proof:

1. 0
   1. Notice that $f(x)=0$ is a continuous function from $[0,1]$
2. Additive Closure
   1. Sum of two continuous functions is continuous
3. Scaler multiplication Closure
   1. A function multiplied by a scaler is still continuous.

Sum of Subspaces

Sum of subspaces is all the possible combinations from the sum of elements from subspaces. Different from union which is very rarely a subspace.

Definition:

Suppose $V_1,V_2,.....,V_n$ are some subspaces of $V$. The sum of $V_1,V_2,.....,V_n$ is noted as $V_1+V_2+.....+V_n$; is the set of all possible sums from the elements from $V_1,V_2,.....,V_n$. I.E: $V_1+V_2+...+V_n=\{v_1+v_2+...+v_3\mid v_1\in V_1,v_2\in V_2,...,v_n\in V_n\}$ Remember, as all subspaces have the $0$ vector we require one element form each as they can have no impact.

Example:

Lets suppose $U,W$ are two subspaces of ${\mathbb{F}}^3$ with the following definitions: $U=\{(x,0,0)\in {\mathbb{F}}^3\mid x\in \mathbb{F}\}\text{and}W=\{(0,y,0)\in {\mathbb{F}}^3\mid y\in \mathbb{F}\}$ Then we can see the sum of subspaces with all possible additions will be: $U+W=\{(x,y,0)\in {\mathbb{F}}^3\mid x,y\in \mathbb{F}\}$ We can verify this with a proof:

1. Let $u\in U$ and $w\in W$. Then we have: $u=(x,0,0)\text{and}w=(0,y,0)$ For some $x,y\in \mathbb{R}$
2. Then notice: $v+w=(x,0,0)+(0,y,0)=(x+0,y+0,0+0)=(x,y,0)$

Lets do another example:

To find the sum of these subspaces kets see the following:

1. Assume $u\in U,w\in W$.
2. Then we can define $u$ and $w$ with the following: $u=(x,x,y,y)w=(a,a,a,b)$ Where $x,y,a,b\in \mathbb{F}$.
3. Then notice $u+v=(x+a,x+a,y+a,y+b)$
4. From this alone it is clear that $U+W\subset \{(x,x,y,z)\in {\mathbb{F}}^4\mid x,y,z\in \mathbb{F}\}$
5. Now for the other direction notice the following for $x,y,z\in \mathbb{F}$: $(x,x,y,z)=(x,x,y,y)+(0,0,0,z-y)=(x,x,y,z)\in U+W$
6. Thus we can conclude $U+W=\{(x,x,y,z)\in {\mathbb{F}}^4\mid x,y,z\in \mathbb{F}\}$

Sum of subspaces is the smallest subspace

This is where the distinction of sum and union is important.

The sum of subspaces is the smallest subspace containing all the summands. This means every subspace containing all the elements of the summands also contains the sum.

Definition:

Suppose $V_1,V_2,.....,V_n$ are some subspaces of $V$. Then $V_1+V_2+...+V_n$ is the smallest subspace of $V$ containing $V_1,V_2,.....,V_n$.

Proof practice

Second part is easy because by definition it is closed under addition so the subspace needs to contain all possible sums of elements.

Direct Sums

Suppose $V_1,V_2,.....,V_n$ are some subspaces of $V$. We already know every element of $V_1+V_2+.....+V_n$ can be written with the form $v_1+v_2+...+v_n$ where each $v_k\in V_k$. However, ones that can only be expressed in one sum form are extremely important and known as direct sums with a special symbol $\oplus$.

Definition

Suppose $V_1,V_2,.....,V_n$ are some subspaces of $V$.

1. Then $V_1+V_2+.....+V_n$ is a direct sum if every element $v_1+v_2+...+v_n\in V_1+V_2+.....+V_n$ can be written only one way as a sum for $v_k\in V_k$
2. A direct sum for $V_1+V_2+.....+V_n$ is denoted by $V_1\oplus V_2\oplus .....\oplus V_n$

Example

Proof:

1. Notice that for any $v\in U\oplus W,v=(x+0,y+0,0+z)=(x,y,z)$ where $x,y,z\in \mathbb{F}$
2. Thus: $U\oplus W=\{(x,y,z)\mid x,y,z\in \mathbb{F}\}$
3. This is precisely the definition of the set ${\mathbb{F}}^3$

Condition to check for direct sum:

To check if something is a direct sum you only need to check the $0$ vector.

Condition:

Suppose $V_1,V_2,.....,V_n$ are some subspaces of $V$. Then $V_1+V_2+...+V_n$ is a direct sum $⟺$ the only way to write the $0$ vector as a sum $v_1+v_2+...+v_n$ for $v_k\in V_k$ is by setting each $V_k$ equal to $0$.

Proof: $\Rightarrow$ $V_1+V_2+...+V_n$ is a direct sum $⟹$ the only way to write the $0$ vector as a sum $v_1+v_2+...+v_n$ for $v_k\in V_k$ is by setting each $V_k$ equal to $0$.

1. Notice that if we sum up the $0$ element from all the included subspaces, we get $0$. Additionally, as this is a direct sum by definition, this is the only way to get $0$

$\Leftarrow$ the only way to write the $0$ vector as a sum $v_1+v_2+...+v_n$ for $v_k\in V_k$ is by setting each $V_k$ equal to $0$ $⟹$ $V_1+V_2+...+V_n$ is a direct sum

1. Assume this were not the case, and there were multiple ways to create $0$, and for some $v_k,u_k\in V_k$ we had it so: $0=v_1+v_2+.....+v_n\text{and}0=u_1+u_2+.....+u_n$
2. Then, subtracting the left equation from the right we get: $0=0-0=(v_1+v_2+.....+v_n)-(u_1+u_2+.....+u_n)=(v_1-u_1)+(v_2-u_2)+...+(v_n-u_n)$
3. Clearly, this means ever $(v_k-u_k)=0$
4. Thus, our theorem still holds.

practice kinda light, the hint is if there are two ways to write it and u add the elements they still ahve to be 0

Condition for two elements:

Suppose $U$ and $W$ are subspaces of $V$. Then $U+W\text{is a direct sum}⟺U\cap W=0$

Polynomials

We define a polynomial as a function ($\mathcal{P}:\mathbb{F}\to \mathbb{F}$ ) with coefficients $a_0,....,a_m\in \mathbb{F}$ such that: $\mathcal{P}(z)=a_0+a_{1}z+a_2{z}^2+....+a_m{z}^m$ for $z\in \mathbb{F}$

With proper notation $\mathcal{P}(\mathbb{F})$ is the set of all polynomials with coefficients in $\mathbb{F}$.

$\mathcal{P}(\mathbb{F})$ is a vector space over $\mathbb{F}$.

You understand deg as the highest non-zero power. However, polynomial of deg 0 is said to have deg $-\infty$.

${\mathcal{P}}_m(\mathbb{F})$ discribes the set of polinomals with at most deg m