Sum of Subspaces

also read 1C. Subspaces

Definition:

Assume that $V_1,V_2,....,V_n$ are subspaces of $V$. Then we can define the sum $V_1+V_2+...+V_n$ as such: $V_1+V_2+...+V_n=\{v_1+v_2+....+v_n\mid v_i\in V_i,i=\{1,2,...,n\}\}$ It is essentially a sum of one element from every subspace, including the 0 vector in every subspace which allow some elements to have no impact.

Examples

Lets do a proof: 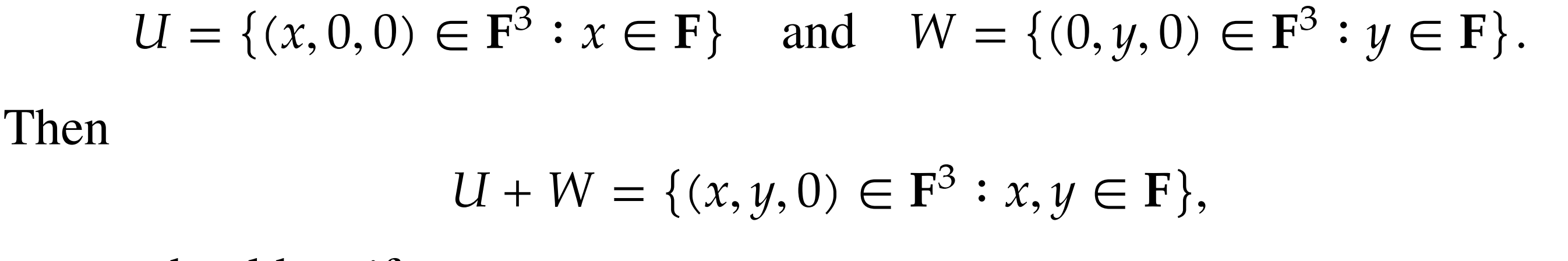Proof: Assume the set on the right where only the 3rd coordinate is 0 is $L$ $U+W\subset L$

1. Let $(u,0,0)\in U$ and $(0,w,0)\in W,u,w\in F$
2. Then: $(u,0,0)+(0,w,0)=(u,w,0)\in L$
3. This holds as the third coordinate is $0$ and all the other elements are in $F$

$L\subset U+W$

1. For any element $(x,y,0)\in L$ we can write it as $(x,0,0)+(0,y,0)$ where $(x,0,0)\in U$ and $(0,y,0)\in W$. Thus this holds. $■$

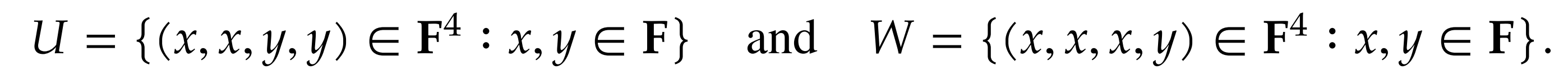
Another example: 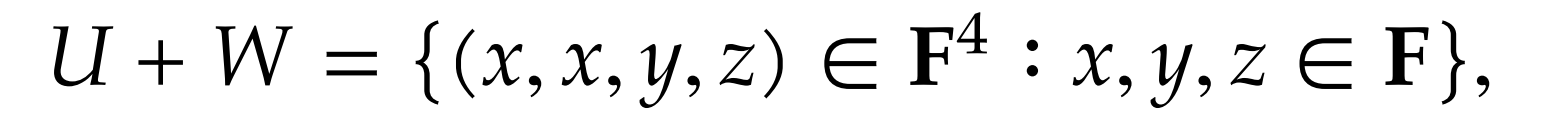Proof: Let the set on the right be known as $L$ $U+W\subset L$

1. Let $(a,a,b,b)\in U$ and $(c,c,c,d)\in W$
2. $(a,a,b,b)+(c,c,c,d)=(a+c,a+c,b+c,b+d)\in L$
3. This holds as the first two coordinates are the same and all coordinates are in $F$ $L\subset U+W$
4. Take any element $(x,x,y,z)\in L$
5. $(x,x,y,z)=(x,x,y,y)+(0,0,0,z-y)$
6. This holds as $(x,x,y,y)\in U$ and $(0,0,0,z-y)\in W$

Another Definition:

Let $V_1,V_2,....,V_n$ be subspaces of $V$. $V_1+V_2+...+V_n$ is the smallest subspace of $V$ containing $V_1,V_2,...,V_n$

Lets prove this in two parts:

1. $V_1+V_2+...+V_n$ is a subspace of $V$
   1. Identity:
      1. Set all $v_i=0$. This is the zero vector as it has to exist in every $V_i$
   2. Additive closure:
      1. Let $v_1+v_2+...+v_n$ and $w_1+w_2+...+w_n$ be elements in the sum for $v_i,w_i\in V_i$. both be elements inside the sum.
      2. Then $(v_1+v_2+...+v_n)+(w_1+w_2+...+w_n)=(v_1+w_1)+(v_2+w_2)+...(v_n+w_n)$
      3. Now this is clearly in the sum as each $v_i+w_i\in V_i$ by its own additive closure.
   3. Scaler Multiplicative Closure
      1. Let $v_1+v_2+...+v_n$ be an element in the sum where every $v_i\in V_i$.
      2. Then for some $\lambda \in F$ we have $\lambda (v_1+v_2+...+v_n)$ which is $\lambda v_1+\lambda v_2+...+\lambda v_n$ by the second distributive property. As every $\lambda v_i\in V_i$ through scaler multiplicative closure, we know the scaler multiple is also in the sum
2. It is the smallest subspace of $V$ containing V_1,V_2,…,V_n
   1. This is clear, as the sum contains all individual elements of each $V_i$ by setting all the other summads to their respective 0. By additive closure the sum of all these elements also has to be in the subspace, thus it needs to include all elements of the sum.