Based on 1A. Preliminaries and Introduction,1B. What is a vector space?, and 1C. Subspaces.
1A
7.
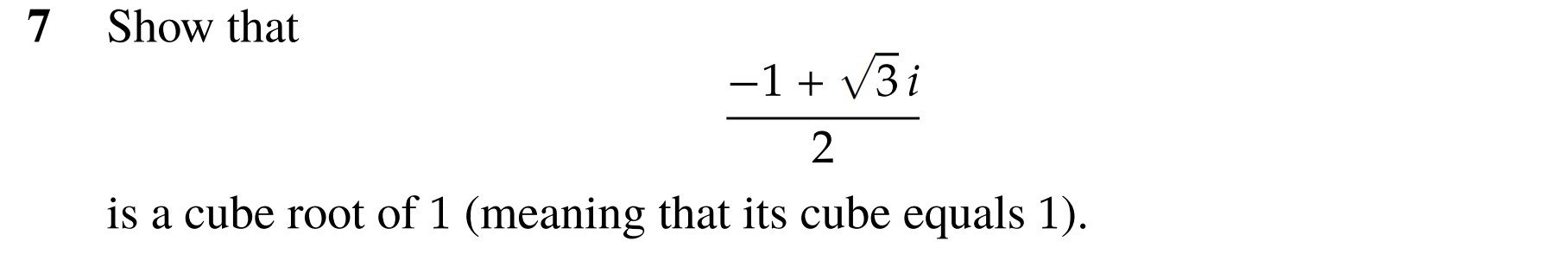 Just algebra
Just algebra
10.
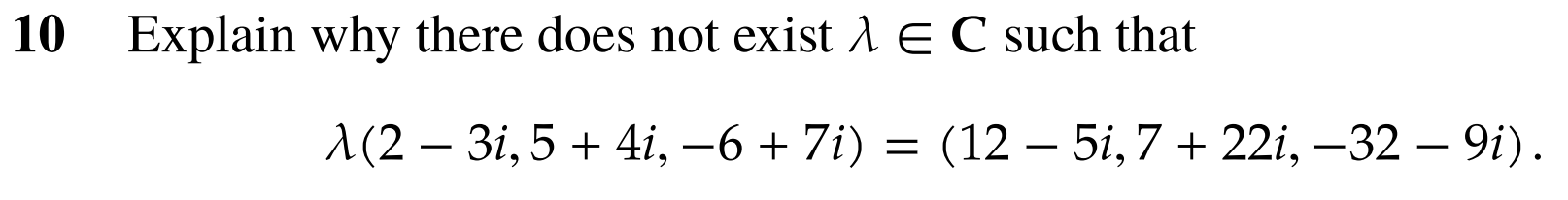 Each factor has to be scaled by the same amount. Lets take the first coordinates to start:
With this, we can see if this works for the rest of the coordinates.
Each factor has to be scaled by the same amount. Lets take the first coordinates to start:
With this, we can see if this works for the rest of the coordinates.
For the second coordinate which does math
For the last coordinate,
The third coordinate does not work as it is plus 9.
1B
1
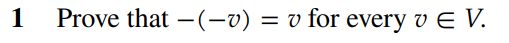 Proof:
Proof:
- Firstly, notice that
- Thus, the additive inverse of is .
4
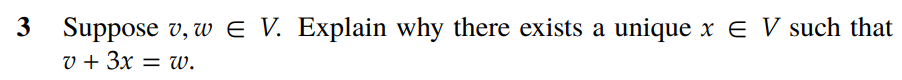 Proof:
Proof:
- First, notice that we can subtract from each side to get the equation:
- Now, as is closed under inverses we know . Additionally as and we know through closure of addition and scaler multiplication must also be in .
- To prove uniqueness, assume that and both satisfy the equation. Then:
- subtracting we get:
- Thus,
- Now multiplying by the scaler we can see:
- Thus and we have proved our is unique.
6.
 Vector spaces have to obay the axioms for vector addition. However notice:
Which is clearly not true as .
Vector spaces have to obay the axioms for vector addition. However notice:
Which is clearly not true as .
8.
 Proof:
Proof:
- Additive Commutativity:
- Let
- Then for some
- Notice:
- by the commutative property of addition we can see the following:
- Additive Associativity:
- Let
- Then
- Notice:
- Additive identity:
- This exists as thus
- Additive inverses:
- Let
- Then for some
- Notice,
- Thus we can see that the inverse of is .
- Additionally, as is a vector space, therefore containing additive inverses for and , it is clear . This means that
- Scaler multiplication associativity:
- Let and
- Let the following definitions hold: For and . Remember is a real vector space
- Given the definition of Complex Scaler Multiplication, notice:
- Now from the other side:
- Skipping this because wtf
- Multiplicative Identity:
- Let for
- Notice:
- Thus scaler multiplication by holds
- Distributive property
- for and
- Let , , and for and
- Notice: #check Fr what is this problem???
- for and
1C
4.
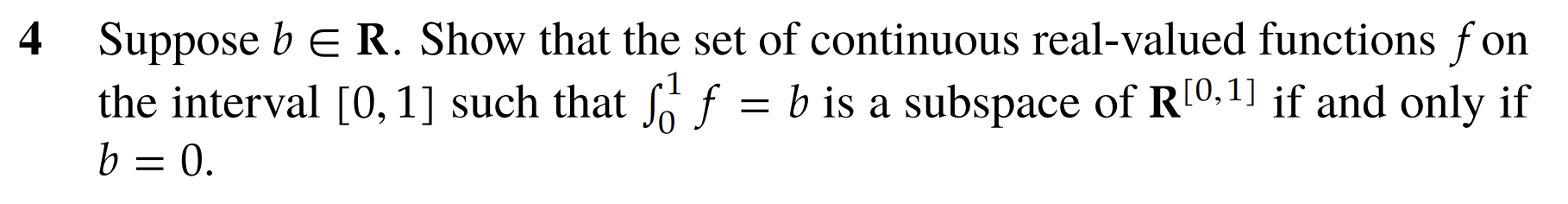 Let
Let
Prove the set of functions over the interval such that is a subspace of
- Assume that the set of functions over the interval such that is a subspace of
- Then, notice that the function must be in the subspace. Thus
- Assume that
- Then the identity is in the subspace as
- For additive closure, assume are in the subspace. This means and .
- Notice, the sum must also be in the subspace as .
- Scaler Multiplication is also closed, as for any in the subspace and , is also in the subspace as :
5.
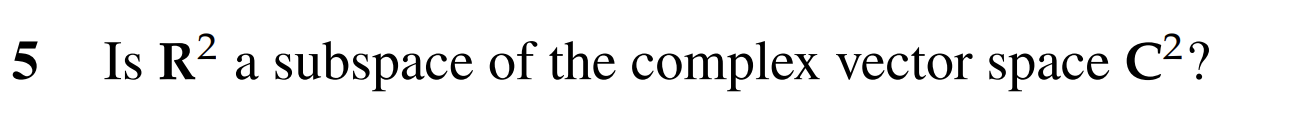 No, it is not. This is because it is not closed under scaler multiplication as we are talking about a complex vector space, for example
No, it is not. This is because it is not closed under scaler multiplication as we are talking about a complex vector space, for example
7.
 No, here is why.
No, here is why.
- This does meet 0 as it is closed under addition and
- This is closed under addition
- This is not closed under scaler multiplication. Lets say you have the subset {-1,0,1}. This is closed under addition and additive inverses. However .
8.
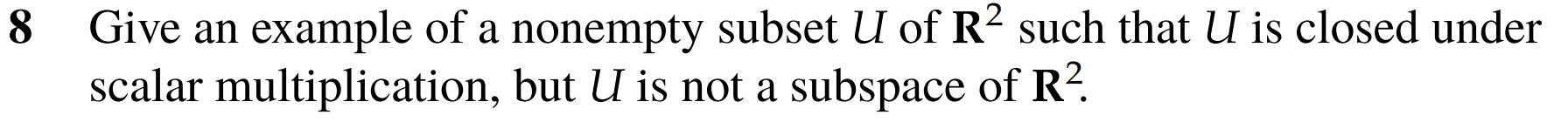
- You can take the two subsets
- Their union is a subset of and closed under scaler multiplcation. However, it is not closed under addition as is not in the union. A better way to say this is one of the coordinates is 0.
11.
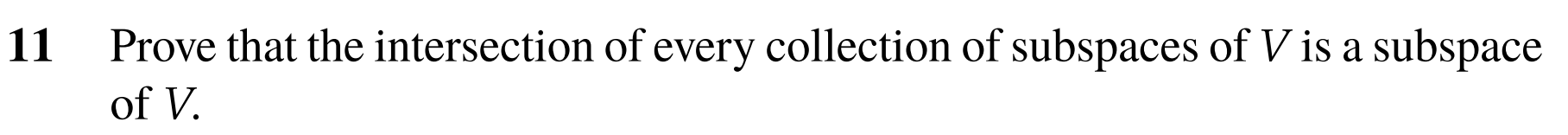 Proof:
1. As 0 is in every subspace, it is in the intersection of all subspaces
2. For additive closure, suppose are in every subspace of . As they are subspaces they must also be closed under addition, which means must also be in every subspace, and therefor the intersection
3. For closure under scaler multiplication, the same logic follows. As every individual vector space is closed under scaler multiplication, so must the intersection. This means that if any element is in the intersection, all of its scaler multiples are also within the intersection as they are also in all the subspaces.
Proof:
1. As 0 is in every subspace, it is in the intersection of all subspaces
2. For additive closure, suppose are in every subspace of . As they are subspaces they must also be closed under addition, which means must also be in every subspace, and therefor the intersection
3. For closure under scaler multiplication, the same logic follows. As every individual vector space is closed under scaler multiplication, so must the intersection. This means that if any element is in the intersection, all of its scaler multiples are also within the intersection as they are also in all the subspaces.
12
 Let be subspaces of
Let be subspaces of
is a subspace of or
- Lets consider the contrapositive:
and is not a subspace of
- This means there is an and an element . Note,
- This means that .
- For the sake of contradiction, assume is a subspace. Then it would have additive closure, and as it must mean that
- This means that either or .
- W.L.O.G assume . Now notice that all the following summands are in :
- However, notice that which is clearly not in . Thus we have reached a contradiction as is a subspace with additive closure.
- Assume or
- Then, if the union is just which is defined as a subspace. Similarly, if the union is just which is defined to be a subspace.