1A. Preliminaries and Introduction

Generalizations

Here are a few generalization for the next few topics that will be explained later:

Vector spaces:

sets with operations of addition and scaler multiplication which satisfy natural algebraic properties.

Subspaces:

Similar to subsets for sets. (Closer to subgroups for groups)

Sums of subspaces are similar to unions of sets

Direct sums of subspaces are similar to unions of disjoint sets.

${\mathbb{R}}^n$ and ${\mathbb{C}}^n$

Skipping over $\mathbb{R}$.

Complex numbers were created to allow for the square root of negative numbers. We already know what $i^2=-1$ is; but for the sake of definitions (mainly for proof writing and rigor) here are the formal definitions of the set $\mathbb{C}$

The set $\mathbb{C}$

1. A complex number is an ordered pair $(a,b)$ where $a,b\in \mathbb{R}$. We often denote them with $a+bi$.
2. The set of all complex numbers is denoted by $\mathbb{C}$. The formal definition is as follows: $\mathbb{C}=\{a+bi\mid a,b\in \mathbb{R},i=\sqrt{-1}\}$
3. Addition and multiplication in $\mathbb{C}$ is defined by (for $a,b,c,d\in \mathbb{R}$): $(a+bi)+(c+di)=(a+c)+(b+d)i$ $(a+bi)(c+di)=ac+adi+cbi-bd=(ac-bd)+(ad+cb)i$ It is clear that $\mathbb{R}\subset \mathbb{C}$ as $\forall x\in R,x=x+0i\in \mathbb{C}$

For some elementary practice (just to warm myself after a summer of no math) here is a practice problem:

$(2+3i)(4+5i)=8+10i+12i-15=(8-15)+(10+12)i=-7+22i$

Basic Arithmetic Properties in $\mathbb{C}$

The common properties of algebra hold for both addition and multiplication

1. Commutativity: $a+b=b+a\text{and}ab=ba\forall a,b\in \mathbb{C}$
2. Associativity: $(a+b)+c=a+(b+c)\text{and}(ab)c=a(bc)\forall a,b\in \mathbb{C}$
3. Identity: $a+0=a\text{and}1a=a\forall a\in \mathbb{C}$
4. Additive Inverses: (note ! means unique) $\forall a\in \mathbb{C}\exists !-a\in \mathbb{C}\mid a+(-a)=0$
5. Multiplicative inverses: $\forall a\in \mathbb{C}\exists !a^{-1}\mid a{a}^{-}1=1$
6. Distributive Property: $a(b+c)=ab+ac\forall a,b,c\in \mathbb{C}$ The rest of this is skipped assuming basic prior knowlage of proofs, definition of subtraction and division.

Other abstract definitions

$\mathbb{F}$

Throughout this course we assume the only fields are real or imaginary numbers, ie $\mathbb{F}=\mathbb{R}$ or $\mathbb{C}$

Scalers

Elements of $\mathbb{F}$ are known as Scalers. Scaler is legit just another word for number:

Scaler is just another fancy term for “number” and is used to distinguish an object from a vector.

Power Rules:

For any $\alpha \in \mathbb{F}$ we can define powers as: ${\alpha }^n=a\cdot a\cdot a\cdot a....\cdot a\text{n times}$ By this definition, it is implied that: $({\alpha }^n{)}^m={\alpha }^{nm}$ and $(\alpha \beta {)}^n={\alpha }^n{\beta }^n$ for all $\alpha \beta \in \mathbb{F}$ and positive integers $n,m$

Lists

To define ${\mathbb{F}}^n$ first look at the following definitions: We can define ${\mathbb{F}}^2$ with the following: ${\mathbb{F}}^2=\{(a,b)\mid a,b\in \mathbb{F}\}$ This is the set of all ordered pair of elements in $\mathbb{F}$. Either real or complex numbers

Similarly, We can define ${\mathbb{F}}^3$ with the following: ${\mathbb{F}}^3=\{(a,b,c)\mid a,b,c\in \mathbb{F}$ This is the set of all complex tuples in $\mathbb{F}$

List Definition:

Let $n$ be a non-negative integer. Then a list of length $n$ is an ordered collection of $n$ elements.

Two lists are equal if and only if they have the same length and the same elements in the same order.

Lists are often denoted by parenthesis and comas; ie a n-length list can look like: $(a_1,a_2,a_3,....,a_n)$ A list of n length is sometimes called an n-tuple.

Sometimes we will refer to a list without explicitly stating a size, however by definition lists are finite length which is a non-negative integer. Therefore an object like $(x_1,x_2,.....)$ is not a list. A list of length zero, denoted as $()$ is also a list.

Lists differ from sets in that:

1. Order matters
2. Repeated elements matter

For example, $(3,5)\ne (5,3)$ however $\{3,5\}=\{5,3\}$

Similarly, $(4,4,4)\ne (4,4)$ however $\{4,4,4\}=\{4,4\}=\{4\}$

${\mathbb{F}}^n$

For the given time, pretend $n$ is some positive integer.

Now, by definition, ${\mathbb{F}}^n$ is the set of all lists of length $n$ with elements in $\mathbb{F}$. ${\mathbb{F}}^n=\{(x_1,x_2,....,x_n)\mid x_k\in \mathbb{F},k=1,2,...,n\}$ And, k defines the coordinate of the list. i.e. for any $x_k$ we say it is the $k$th element

For $n\ge 4$ we cannot visualize ${\mathbb{R}}^n$ as a physical object, it is only possible in 3 dimensions.

Similarly, we can not visualize ${\mathbb{C}}^n$ as an physical object for $n\ge 2$. However, ${\mathbb{C}}^1$ can be thought of as a plane.

Addition in ${\mathbb{F}}^n$.

Addition in ${\mathbb{F}}^n$ is defined by adding corresponding values.

$$(a_1,a_2,...,a_n)+(b_1,b_2,...,b_n)=(a_1+b_1,a_2+b_2,....,a_n+b_n)$$

We can just use variables to denote lists to simplify proofs:

Lets do the following proof:

If $x,y\in {\mathbb{F}}^n$ then $x+y=y+x$ Proof:

1. First let $x=(x_1,x_2,...,x_n)\in {\mathbb{F}}^n$ and $y=(y_1,y_2,...,y_n)\in {\mathbb{F}}^n$
2. Now notice x+y = (x_1,x_2,...,x_n) + (y_1,y_2,...,y_n) = (x_1+y_1,x_2+y_2,....,x_n+y_n)$$$$= (y_1+x_1,y_2+x_2,....,y_n+x_n) = (y_1,y_2,...,y_n) + (x_1,x_2,...,x_n) = y+x
3. Through commutativity of addition, it follows that these are the same. Hense $x+y=y+x$. Thus proved.

For prewriting, aim to work with just $x$ without coordinates when possible. If coordinates are needed, use $x$ with different subscripts to denote coordinates. i.e. for $x\in {\mathbb{F}}^n$ aim to use just $x$; however if coordinates are needed use $x=(x_1,x_2,...,x_n)$.

0

Let 0 denote the list of elements with the value 0. i.e.: $0=\{0,0,....,0\}\in {\mathbb{F}}^n$ Note these are not the same. The 0 on the left denotes a list, while the 0s within the set define the element $0\in \mathbb{F}$

Vector Spaces Graphical Intuition

Addition

We can think of elements of ${\mathbb{R}}^2$ as Points or Vectors. For example, lets notice the following vector: $(a,b)=v\in {\mathbb{F}}^2$ We can represent this as a point or vector with the following:

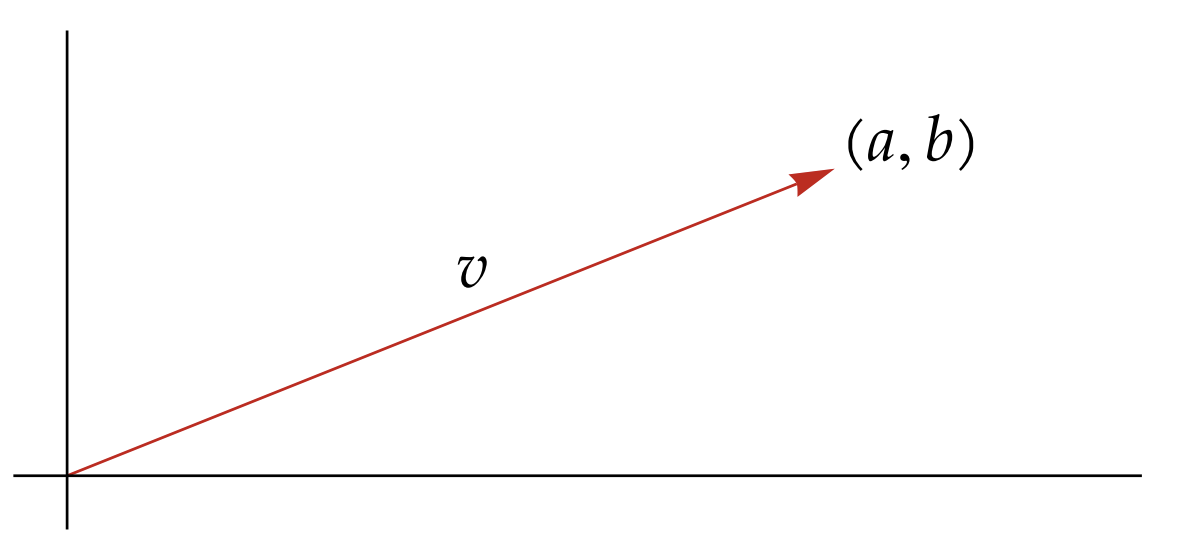
If we are thinking of it as a point, we will just think of the usual point $(a,b)$

If we are thinking of it as a vector we will think of the line starting from the origin and then ending at $(a,b)$.

If we are referring to elements as vectors, the following are the same vector (arrow parallel to its-self): 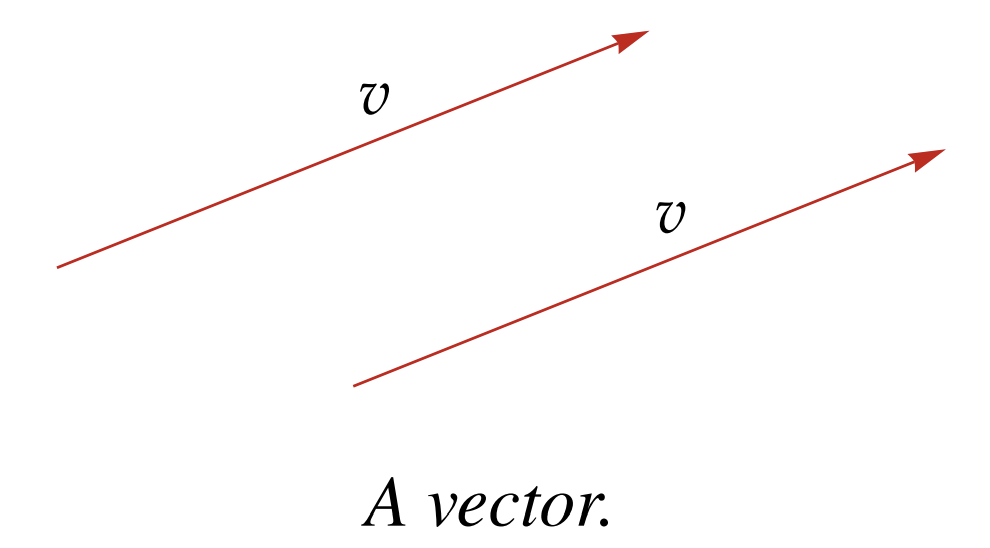This is because they have the same length and direction.

The reason vector addition works is because if we place $v$ parallel to itself and move the starting point to the endpoint of $u$, their addition leads to the same point in the plane: 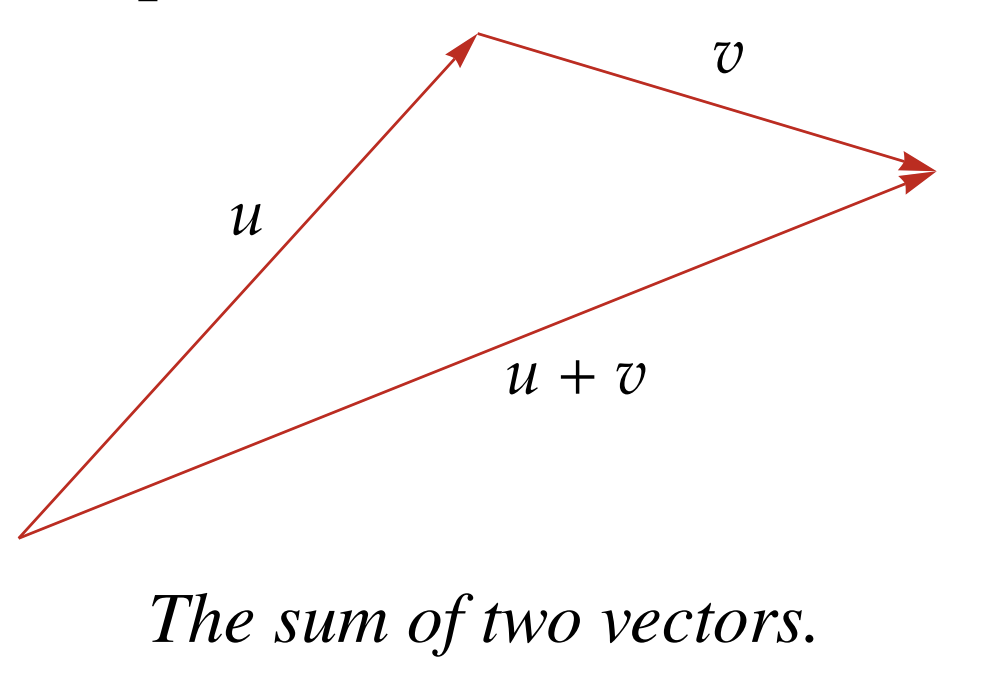Notice how the start point of vector $u+v$ is the same start point as $u$ but end point of the vector is the same endpoint as $v$.

Additive inverses in in ${\mathbb{F}}^n$

For any $x\in {\mathbb{F}}^n$ the additive inverse is just $-x$ (scaler multiplication of $-1$ and $x$)as: $x+(-x)=0$ And notice if we define $x$ as: $x=(x_1,x_2,....,x_n)$ then we have to define $-x$ as: $-x=(-x_1,-x_2,....,x_n)$ and by this definition, we are just setting every coordinate to $0$. Thus $-x$ is the additive inverse.

Essentially its a vector of the same length pointing in the opposite direction. We can view it from the image below: 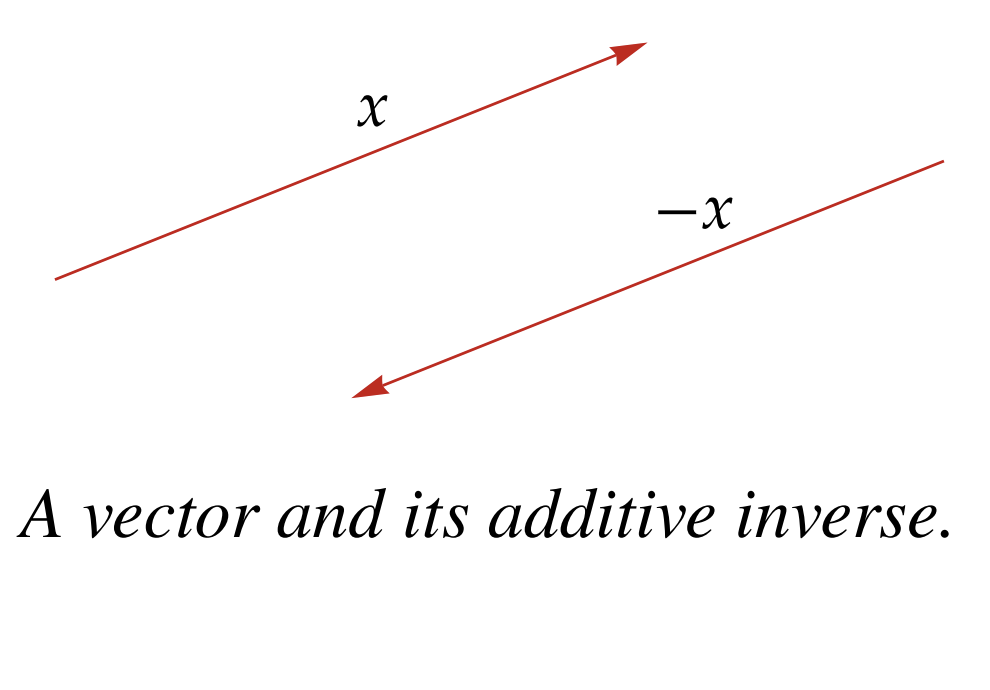Notice this fits with our previous understanding of geometric notation, as adding this together geometrically will lead you back to the point or vector 0 (legit origin for point, and an arrow that goes in neither direction for vector).

Multiplication

We are interested in scaler multiplication, which is multiplying a vector in ${\mathbb{F}}^n$ with a scaler in $\mathbb{F}$

By definition, for a vector element $(x_1,x_2,....,x_n)\in {\mathbb{F}}^n$ and a scaler element $\lambda \in \mathbb{F}$ we define scaler multiplication with the following: $\lambda (x_1,x_2,....,x_n)=(\lambda x_1,\lambda x_2,....,\lambda x_n)$

You can also view this scaler geometrically and it works out extremely well: You are legit scaling the vector with a factor of the scaler.

Fields

Also view Fields

However, by the definition in LADR: A Field is a set which:

1. Contains distinct elements 0 and 1
2. Contains usual arithmetic properties of addition and multiplication (used when we defined $\mathbb{C}$)