Section 9

Limit theorem for sequences

Convergent sequences are bounded

I will go over this proof in order to warm up, however I will skip the rest as they are extremely trivial results from calculus.

Assume that $s_n$ is a convergent sequence. This means, for ever $ϵ$ there exists an $N$ such that $n>N⟹|s_n-s|<ϵ$

For now, pick $ϵ=1$, thus there is some $N$ where $n>N⟹|s_n-s|<1$ Now, notice that we can define $|s_n|=|s_n-s+s|\le |s_n-s|+|s|$ We can further this to show $|s_n|\le |s_n-s|+|s|<1+|s|$ by combining it with our first inequality. Now we know $|s_n|<|s|+1$

Putting all this together, remember $M$ denotes an upper bound. Thus, let $M=\max \{|s|+1,s_1,s_2,\dots ,s_N\}$. For all $|s_n|,n>N$ we already know its bounded by $|s|+1$. For the other $n$ before $N$ we include them as bounds. Remember, its an upper bound if every element is less than or equal to $M$

Limit properties

1. If $s_n\to s$ then $k{s}_n\to ks$ Another way of writing this is $\lim k{s}_n=k\lim (s_n)$
2. If $s_n\to s$ and $t_n\to t$ then $(s_n+t_n)\to (s+t)$ Another way of writing this is $\lim s_n+t_n=\lim (s_n)+\lim (t_n)$
3. If $s_n\to s$ and $t_n\to t$ then $(s_n{t}_n)\to (st)$ Another way of writing this is $\lim s_n{t}_n=\lim (s_n)\lim (t_n)$
4. If $s_n\to s$ then $\frac{1}{s_n}\to \frac{1}{s}$ provided that $s_n\ne 0\forall n$ and $s\ne 0$
5. If $s_n\to s$ and $t_n\to t$ then $\frac{t_n}{s_n}\to \frac{t}{s}$ provided $s_n\ne 0\forall n$ and $s\ne 0$

For 4 and 5, we add extra conditions to avoid a divide by $0$ error.

Now here are some basic limits that should be familiar to you from calculus:

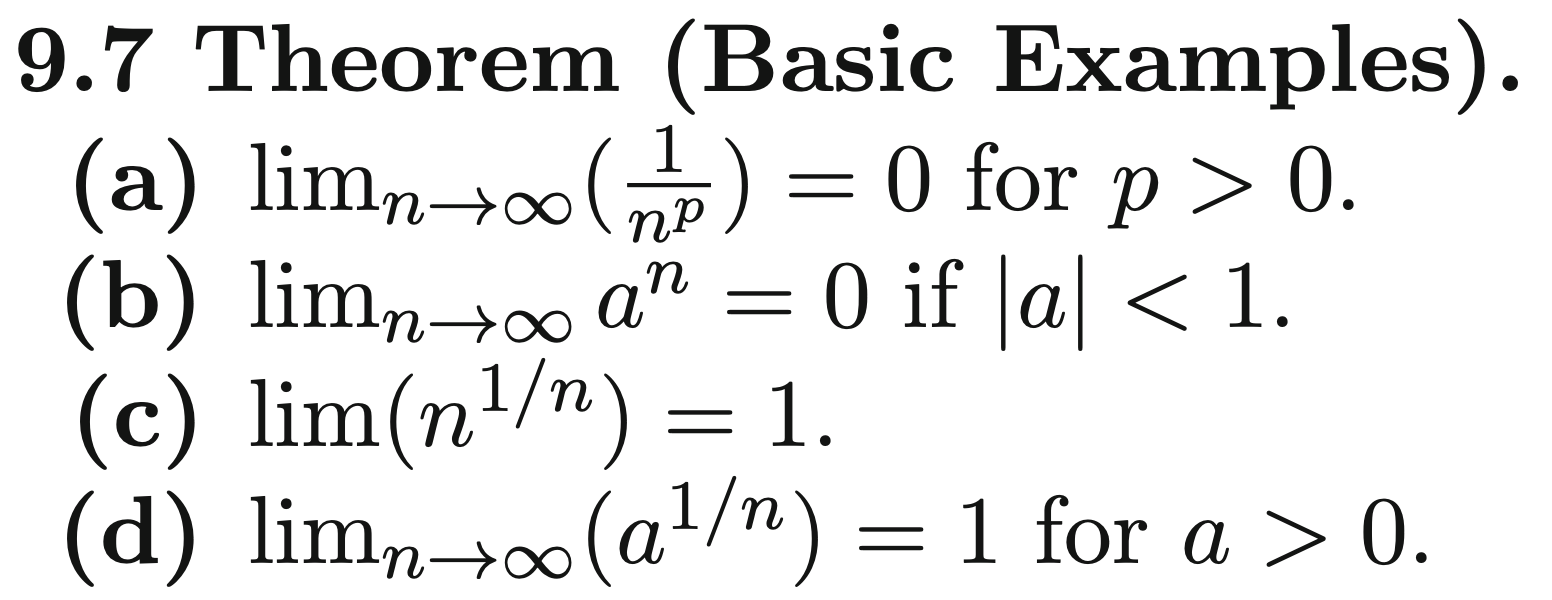
These should be really easy so I will do a couple:

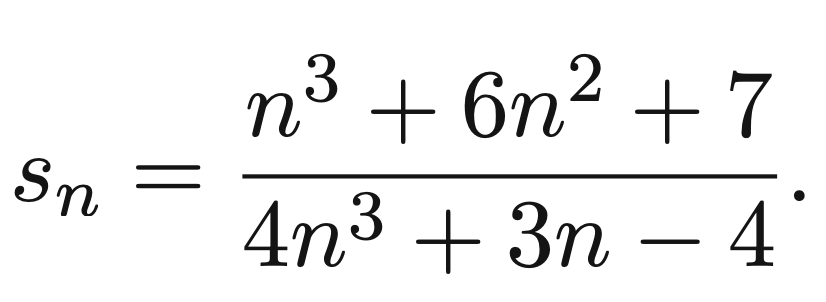
This is equivalent to saying $\frac{1+\frac{6}{n}+\frac{7}{n^3}}{4+\frac{3}{n^2}-\frac{4}{n^3}}$ And then, for large n all elements go to 0 apart from $\frac{1}{4}$

Formal definition of limit to infinity

For any sequence $(s_n)$ we can write $s_n\to \infty$ provided that for each $M>0$ there is a number $N$ such that $n>N⟹s_n>M$

In other words, for every supposid upper bound we can take, the sequence crosses it after a certain $N$

There is a similar definition for $-\infty$: For any sequence $(s_n)$ we can write $s_n\to -\infty$ provided that for each $M<0$ there is a number $N$ such that $n>N⟹s_n<M$.

The challenging values for these proofs are extremely large $M$ for positive infinity, or extremely small $M$ for negative infinity.

Note, some limits do not converge OR go to any infinity. Such as $(-1{)}^n$. Taking the limit of these is pointless.

A limit only exists if it converges to some point, or diverges to some infinity.

Proofs involving limits to infinity.

These are extremely similar to proofs we did before. Lets take a look: 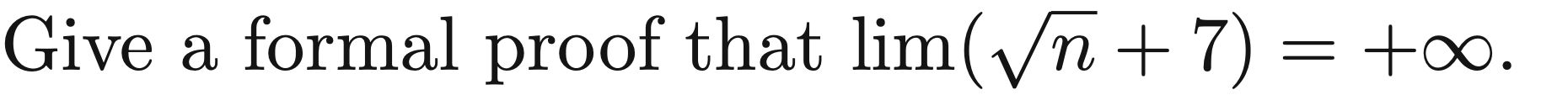By definition, we need to show that for any $M>0$ there exists some $N$ where $n>N⟹\sqrt{n}+7>M$.

To find this $n$ we work backwards then write the proof: $\sqrt{n}+7>M⟹\sqrt{n}>M-7⟹n>(M-7{)}^2$

Thus we are ready to write the proof

1. Let $M>0$ and $N=(M-7{)}^2$
2. Then, for any $n>N$ we see that $n>(M-7{)}^2$
3. This implies that $\sqrt{n}>M-7⟹\sqrt{n}+7>M$
4. thus, we have showed that for any $M>0$ there exists $N=(M-7{)}^2$ where $n>N⟹\sqrt{n}+7>M$. This shows that the limit diverges to $\infty$.

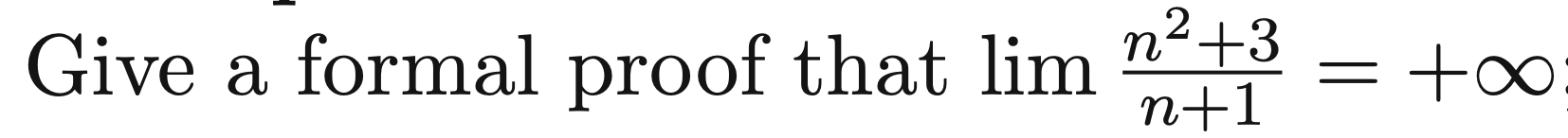We want to show for any $M>0$ there exists an $N$ such that $n>N⟹\frac{n^2+3}{n+1}>M$.

Again working backwards, $\frac{n^2+3}{n+1}>M$, we know that $n^2+3>n^2$ and $n+1<2n$. Thus, $\frac{n^2+3}{n+1}>\frac{n^2}{2n}=\frac{n}{2}>M$.

This we only need to show $\frac{n}{2}>M$ which can be done easily by $n>2M$

Formal proof:

1. Let $M>0$ and $N=2M$
2. Then, for any $n>N$ we have it so $n>2M$
3. this implies that $\frac{n}{2}>M$
4. Furthermore, notice that $\frac{n}{2}=\frac{n^2}{2n}>M$
5. $\frac{n^2+3}{n+1}>\frac{n^2}{2n}>M$
6. Thus $n>N⟹\frac{n^2+3}{n+1}>M$ as $n^2$ is a lower bound for $n^2+3$ and $2n$ is an upper bound for $n+1$

Infinite limit theorems:

Let $s_n$ and $t_n$ be sequences such that $\lim s_n=\infty$ and $\lim t_n>0$ or is $\infty$. Then $\lim s_n{t}_N=\infty$.

Lets use the theorem to prove the following: 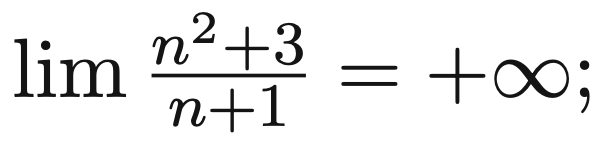We basically separate this into $(n+\frac{3}{n})(\frac{1}{1+\frac{1}{n}})$ As it is easy to show $(n+\frac{3}{n})\to \infty$ and $(\frac{1}{1+\frac{1}{n}})\to 1$ we can use the theorem above to show the product goes to $\infty$.

For a sequence $s_n$ of positive real numbers, $s_n\to \infty ⟺(\frac{1}{s_n})\to 0$