Section 5

$\infty$ and $-\infty$

Both $\infty ,-\infty$ are not real numbers. This is important as this means theorems and exercises do not include $\infty$. However, we can ajoin these elements to the set $\mathbb{R}$ and allow us to use them how we usually do.

That is, for any element in $\mathbb{R}$ we know it is greater than $-\infty$ but less than $\infty$.

Then the set builder notation interval works as expected

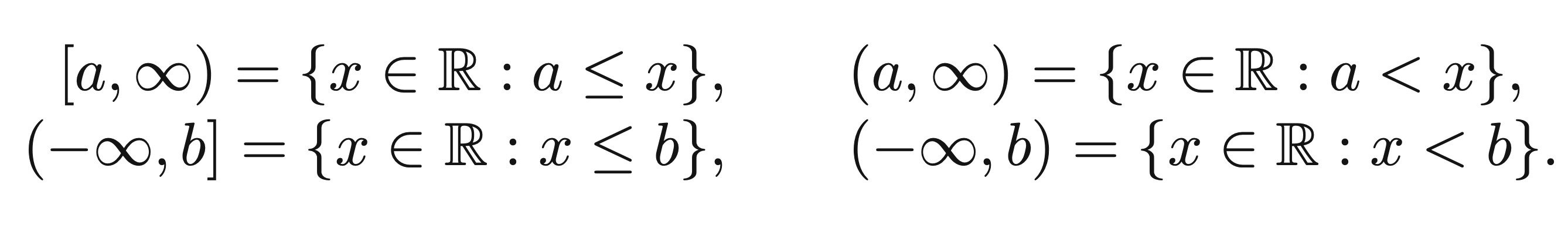
We can also denote $\mathbb{R}=(-\infty ,\infty )$.

If $S$ is not bounded from above or bellow we can define $\text{sup }S$ and $\text{inf }S$ to be $\sup S=\infty \text{and}\inf S=-\infty$

Even with this notation we know that $\inf S\le \sup S$ for all subsets of $\mathbb{R}$.

todo last proof, which works after a question in section 4

todo also do question from section