1. Scratch work
We need to show that for any there exists some such that .
Lets start off with the ending and work backwards. . Notice that for . Then it is sufficent to prove that . This is true for
Proof:
Scratch work
We need to show that for any there exists some such that .
Lets start off with the ending and work backwards. . Notice that for . Then it is sufficent to prove that . This is true for
Proof:
- Let and
- Then, for any we have and
- Notice,
- Thus, for any we have an such that
2.
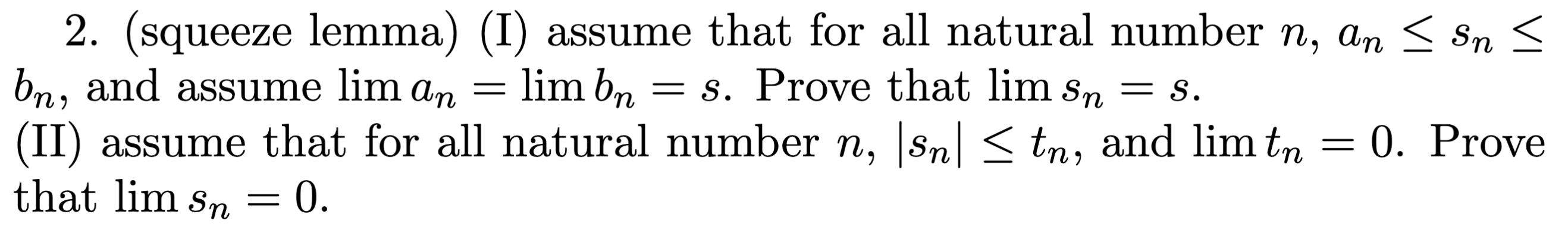 finished on ipad
finished on ipad
3.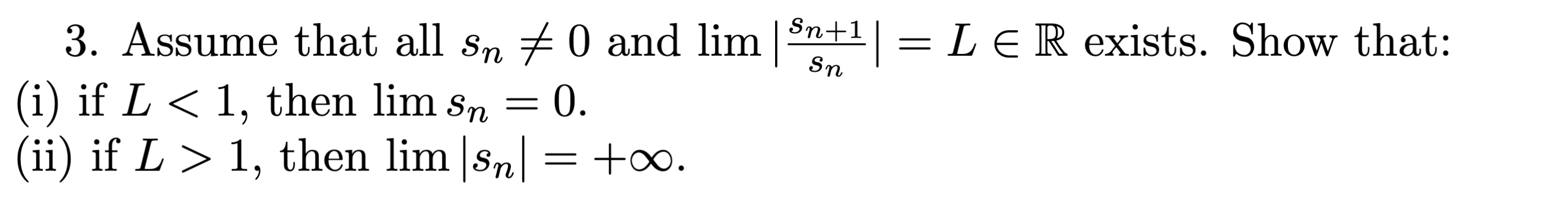 #todo
4.
#todo
4. finished on ipad
5.
finished on ipad
5.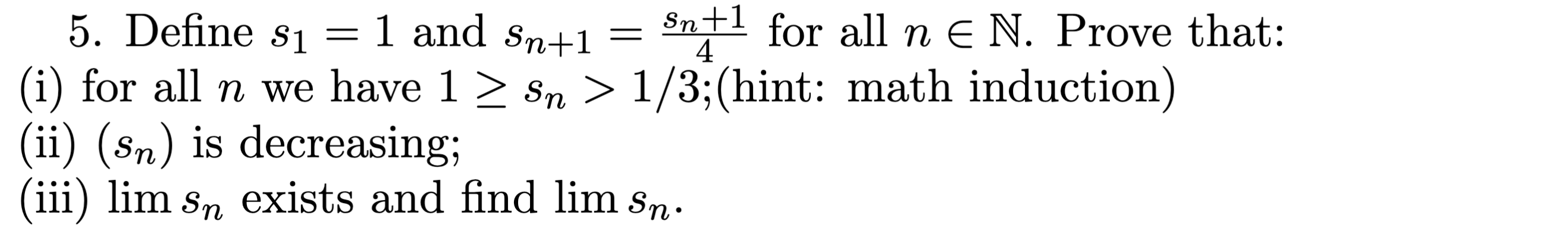 im gonna skip because fuck induction.
im gonna skip because fuck induction.