Work is shown on page 449
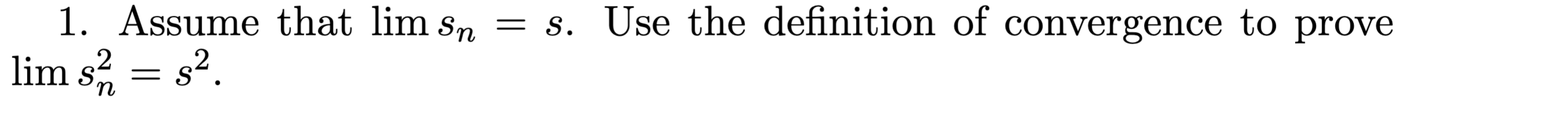 #todo
#todo
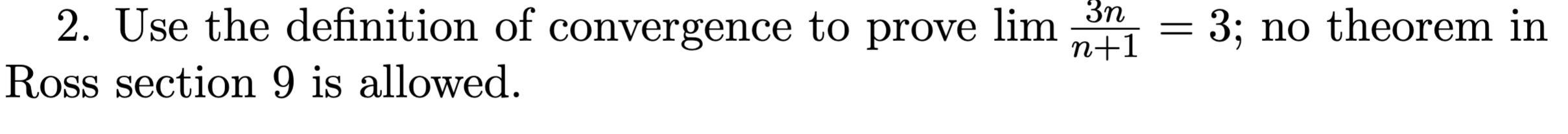 Proof:
Proof:
- Assume
- Then lets pick
- For any
- This implies that
- Meaning,
- Notice
- Thus For any there exists an such that . By the limit convergence theorem this holds.
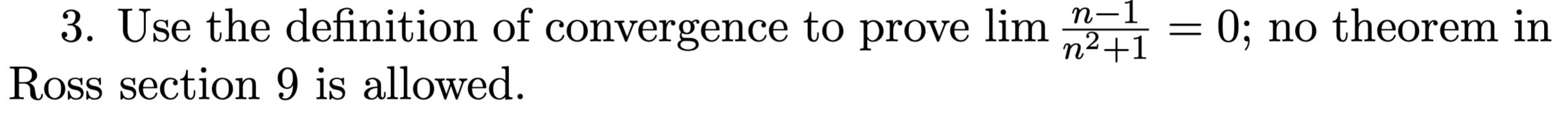 Proof:
Proof:
- Assume
- Then, lets pick
- Then, for we have
- This implies that
- Notice that
- As can confidently say
- Thus, we have shown for all there exists an such that implies . By the convergence definition this sequence converges.
 #todo
#todo
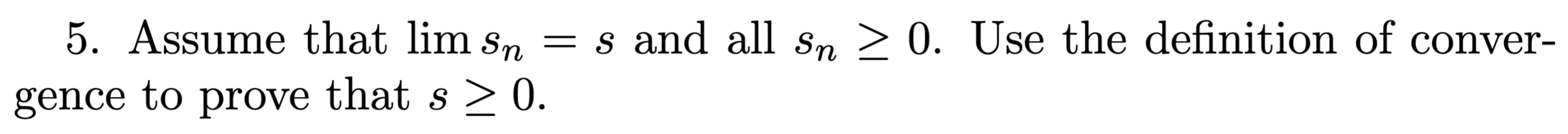 Proof:
Proof:
- Assume and all
- Then for all we know there exists such that
- For the sake of contradiction, assume . Then we can set
- .
- Then, we have it so . This is a contradiction as it implies .