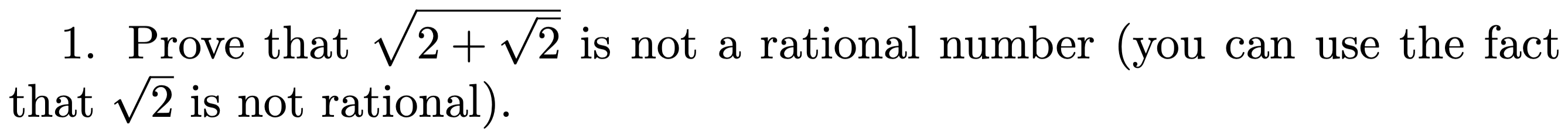
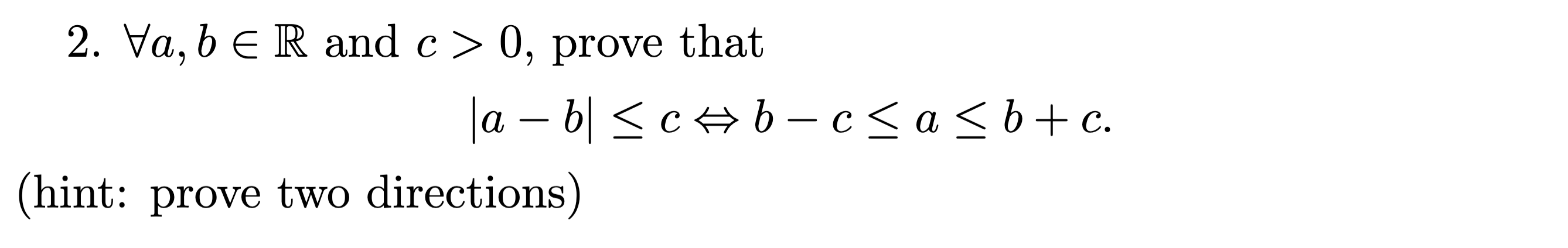 Proof:
Proof:
-
- Assume for some positive
- then . Adding to each side we get
-
- Assume
- Then, subtracting from both sides we get
- thus .
 Proof
Proof
- As both the previous sets are bounded, let be and respectively. Then, w.l.o.g assume . With this, it stands that will also be an upper bound of as it is larger than any element in that set. Taking any element , either or . Then, if we have it so . If , we have it so , thus it is bounded by . Use the same logic for infimum.
- W.L.O.G assume . Then, by definition it is smaller than any element in . It is also smaller than any element in because for any we have it so . Thus, is a lower bound for . Now assume there was another lower bound of . Then because its the greatest lower bound of and . By definition it is the greatest lower bound of , and if there was a greater bound then either , which means there are such elements in which are less than serving as a contradiction, or which means there are elements in both and that are less than .
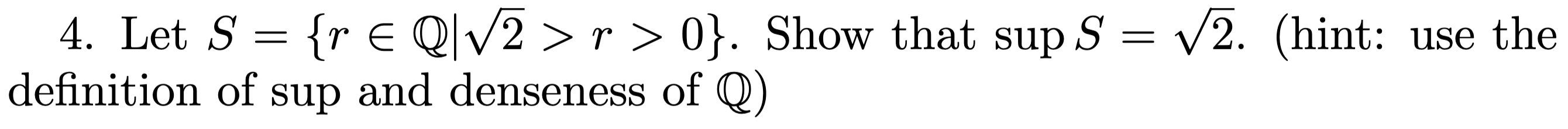 Proof:
Proof:
- Firstly, notice that is an upper bound, by definition. Now, for the sake of contradiction, assume there is another upper bound . Then, by the density of , since both and are real numbers, there exists a rational between and serving as a contradiction for being an upper bound.
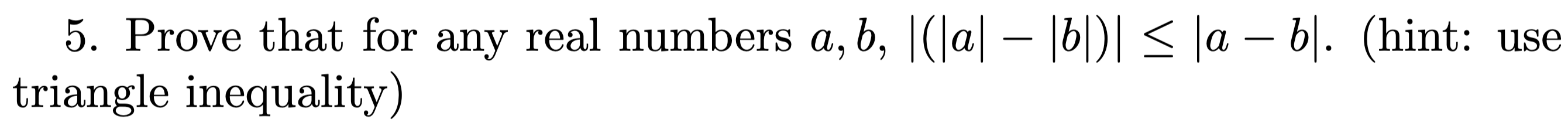 Proof: todo hint: show the other expanded form, include triangle inequality with something like
Proof: todo hint: show the other expanded form, include triangle inequality with something like