Rings

Ring Basics

A set is a ring if it is an abelian additive group with multiplicative associativity and the distributive property. A ring with 1 is called a ring with unity/identity. A ring with multiplicative community is called a commutative ring. Most rings we work with are commutative rings with identity. A commutative ring with identity is an integral domain if when ab=0 either a = 0 or b = 0. A ring is a division ring if every non-zero element is a unit (multiplicative inverse of another). A commutative division ring is a Field.

Types of rings:

$\mathbb{Z}$ is an integral domain (no multiplicative inverses. i.e. for $2\in \mathbb{Z}$ we have $\frac{1}{2}\notin \mathbb{Z}$)

$\mathbb{R},\mathbb{Q},\mathbb{C}$ are all Fields.

${\mathbb{Z}}_n$ is a commutative ring. ${\mathbb{Z}}_p$ is a field

Clearly ${\mathbb{Z}}_n$ is a commutative ring, however it is not an integral domain unless n is prime. For prime n it is a field.

Subrings:

Chain of subrings:

It is clear to see $n\mathbb{Z}$ is a subring of $\mathbb{Z}$
Additionally:

Proposition for subrings:

Let S be a subset of ring R, $S\subset R$. Then, S is a subring iff:

1. $S\ne \mathrm{\varnothing }$ (S is not empty)
2. $s_1{s}_2\in S\mathrm{\forall }{s}_1,s_2\in S$ (S has multiplicative closure)
3. $s_1-s_2\in S\mathrm{\forall }{s}_1,s_2\in S$ (Reverse additive closure)

Integral Domain and Fields (Intro)

Two elements $a$ and $b$ are zero devisors in a commutative ring if $ab=0$ but $a$ and $b$ are both not 0. Fields are commutative division rings. An integral domain has non zero devisors.

A Set $F$ is a field if and only if:

1. $F$ is an additive abelian group
2. $F$\{0} is a multiplicative abelian group
3. Distributive property. Left and right.

Gaussian Integers ring $\mathbb{Z}[i]$

Note, $i^2=-1$ thus all elements in this ring are deg 1, ie

$\mathbb{Z}[i]=\{a+bi\mid a,b\in \mathbb{Z}\}$

It is clear to see $\mathbb{Z}[i]\subset \mathbb{C}$ (note does not contain all complex numbers). #review
(Ex 16.12; skipping over this but go through the example.)

This set in ${\mathbb{M}}_2({\mathbb{Z}}_2)$ Forms a field:

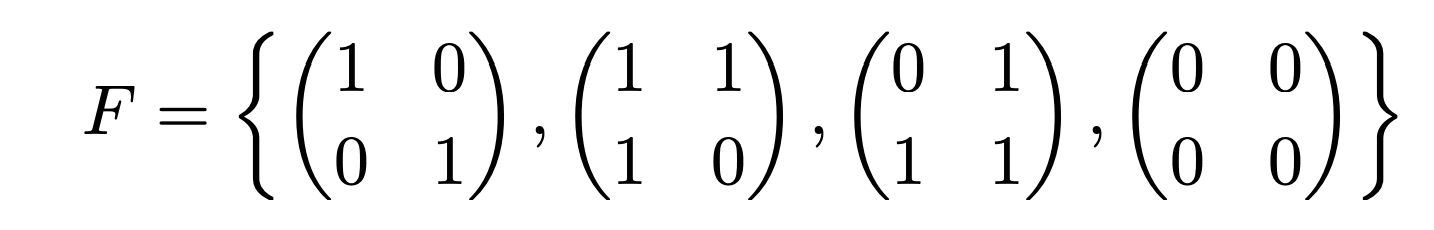
This is extremely specific, idk if i need to go through it rigorously

$\mathbb{Q}[\sqrt{2}]$ forms a field

Remember, ${\sqrt{2}}^2$ is 2 so every element here is of deg 1

#quick_review ex16.14. What are the inverses?

Important theorems for integral domains:

Cancelation Law: (Check for integral domain)

Let $D$ be a commutative ring. $D$ is an integral domain $⟺$ for all non-zero $a\in D$ if $ab=ac, b=c.

Every Finite integral domain is a field

Characteristic:

The Characteristic for $R$ is the least positive integer in $R$ such that $nr=0$ for all $r\in R$. If one does not exist then characteristic of $R$ is $0$. Notated char $R$

Characteristic of ${\mathbb{Z}}_p$:

From the definition, it follows that the characteristic of every ${\mathbb{Z}}_p$ is $P$

Order -> Characteristic association.

For any ring $R$ with identity, if 1 has order n then the characteristic is n as n1 = 0. Or:

For any element $r\in R$. This means the characteristic of a commutative ring with identity is the order of 1

Characteristic of an Integral Domain is always prime

if not 0.

Ring homomorphisms and Ideals

Homomorphisms

Ring homomorphisms are the same, but now must carry addition and multiplication. An isomorphism again is just a bijective homomorphism.

Kernel of the homomorphism is again just the set of elements that map to 0 though the homomorphism.

For any n there is a homomorphism $\mathrm{\Phi }:\mathbb{Z}\to {\mathbb{Z}}_n$ by $\mathrm{\Phi }(a)=a(modn)$

#review evaluation homomorphisms ex 16.21

Homomorphisms carry:

1. Commutative property
2. Multiplicative and Additive identities
3. Field

Ideal

Subring $I$ such that both $ri$ and $ir$ are in $I$; i.e.:
$rI\subset I$ and $Ir\subset I$. One or the other is noted as left or right ideal.
(Remember, you have to show I is a subring first). Similar to normal subgroups

If you have a subset instead you can use the following definition:

1. $I$ is closed under addition
2. $ri\in I$ for all $r\in R$ and $i\in I$. Should do both directions for commutative rings

Trivial ideals:

$\{0\}$ and then ring itself $⟨1⟩=R$

Principal ideals

is a ideal for some $a\in R$. In a commutative ring with identity this is the principal ideal.

Additionally, the trivial ideals are principal.

Ever ideal in $\mathbb{Z}$ is principal

We will come back to this, especially $\mathbb{Z}$ is a PID

The only ideals of $\mathbb{Z}$ are $n\mathbb{Z}$

Combine the following:

The kernel of any ring homomorphism is an Ideal.

For ideal I of R, there is a ring homomorphism from $\psi :R\to R/I$ defined by $\psi (r)=r+I$ where the kernel is $I$ (as any element would lead to just $I$ which is the additive identity of $R/I$)

Factor Groups:

For some ideal $I$ of $R$, the factor group $R/I$ is a ring with multiplication definition

First Iso Theorem; works exactly the same as in groups.

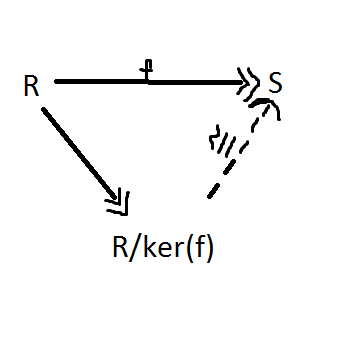
Correspondence theorem

#review needed for a midterm 2 question you could not solve. Theorem 16.34

Maximal and Prime ideals

Maximal and prime ideals allow us to characterize $R/I$ as a integral domain or field.

Maximal Ideal:

A proper ideal $M$ of a ring $R$ is a Maximal Ideal of $R$ if $M$ is not a proper subset of any ideal of $R$ other than $R$ its-self.

Note: I hate this book definition so here is a different one I included from Half-Factorial Domains

If $I$ is a maximal ideal, for every $J$ ideal s.t. $I\subseteq J\subseteq R$ , then $J$ is either $R$ or $I$.

Does not mean the largest ring (I think)

Prime Ideal:

An ideal P is prime iff whenever $ab\in P$ either $a\in P$ or $b\in P$

Important theorems:

For commutative rings with identity: (important for next proof.)

1. $I$ is prime $⟺$ $R/I$ is a Integral Domain.
2. $I$ is maximal $⟺$ $R/I$ is a field.

For ideal $p\mathbb{Z}$ in $\mathbb{Z}$ with prime p, $p\mathbb{Z}$ is a maximal ideal:

Take the factor group $\mathbb{Z}/p\mathbb{Z}$. This is isomorphic to ${\mathbb{Z}}_p$ which is a field. This $p\mathbb{Z}$ must be prime maximal.

The isomorphism makes sense too as cosets are just multiples of p, multiples of p +1, etc until p-1.

Ideals in ${\mathbb{Z}}_n$

All ideals are generated by an element a which is a factor of n.

Every maximal ideal in an commutative ring with identity is also prime as every field is also an integral domain.

Reading Questions:

1. What is the fundamental difference between groups and rings?
   1. Rings also have multiplicative associativity and the distributive property.
2. Give two characterizations of an integral domain.
   1. If ab=0, then a = 0 or b = 0. Integral domains are commutative rings with identity.
3. Provide two examples of fields, one infinite, one finite
   1. Infinite: $\mathbb{R}$
   2. Finite: ${\mathbb{Z}}_7$ or any ${\mathbb{Z}}_p$ for prime p.

Polynomials:

Define polynomial multiplication and addition the usual way. Many of these are familiar so I am speed-running. Review proofs if needed.

If $R$ is a commutative ring with identity then $R[x]$ is a commutative ring with identity.

In $R[x]$ where R is an integral domain, the degree of the product of two polynomials is their sum.

Remember, this is only true in integral domains R, doesn't say much about $R[x]$.

$(x^2+3)(x^3+x^2+34)=x^5...$

There is a homomorphism from $R[x]\to R$

Evaluation homomorphism ${\psi }_{\alpha }:R[x]\to R$ exists defined by ${\psi }_{\alpha }(p(x))=p(\alpha )$. Called the evaluation homomorphism. These are surjective

Division Algorithm:

Similar to integers:

Any polynomial p(x) can be written as:
$p(x)=q(x)g(x)+r(x)$
where the deg of r(x) is less then the quotient or 0.

An element $\alpha$ is a zero $⟺$ $(x-\alpha )$ is a factor.

Most amount of zeros = degree of polynomial

Irreducible Polynomials:

Can not be shown as a factor of polynomials with smaller degrees within the same field F

#review Most of the rest of 17. Skipped because it does not seem extremely important, however might need to go back.

Ideals in $F[x]$

Note: $F$ being a field does not mean $F[x]$ is a field. It is a PID

Generated (principal):

$⟨a(x)⟩=\{a(x)f(x)\mid f(x)\in F[x]\}$

$F[x]$ is a PID

#review Maybe do the proof? see why this is?

Ie, $⟨x^2⟩$ is the ideal with all polynomials without x and c

${\mathbb{F}}_p\cong {\mathbb{Z}}_p$ for prime p.

Note, does not work for not prime P as then ${\mathbb{Z}}_n$ would not be a field. Additionally, remember ${\mathbb{F}}_{p^n}\cong GL(p^n)$, so its only a field if there are $p^n$ elements (power of some prime.)

Let $F$ be a field and let $p(x)\in F[x]$. Then:

1. $<p(x)>$ is maximal $⟺$ p(x) is irreducible.
   You can combine this with [[#Important theorems]] to show a iff chain in fields:
2. $p(x)$ is irreducible in $F[x]$ $⟺$ $⟨p(x)⟩$ is maximal $⟺$ $F[x]/⟨p(x)⟩$ is a Field
   Note: The second part of this works in any commutative ring with identity. The first part is only for a field.
   #important

Example Questions for this theorem:

You can use this to answer the warm up from April 28th:
I will solve it here:
Prove that the following are all fields:

1. $\mathbb{Q}[x]/⟨x^2-2⟩$
   1. We are already aware that $\mathbb{Q}$ is a field. Thus, taking $x^2-2$ we can see that the only solutions of this are $\pm \sqrt{2}$. Both of these are irrational, thus $x^2-2$ is irreducible. This is because, by the division algorithm all factors must be of deg 1 (ie $x-\alpha$), and such a factor would exist iff it were a zero. Now, $x^2-2$ being irreducible means $⟨x^2-2⟩$ is maximal meaning $\mathbb{Q}[x]/⟨x^2-2⟩$ is a field.
2. $\mathbb{Q}[x]/⟨x^3-2⟩$
   1. Similarly, $\mathbb{Q}$ is a field. $x^3-2$ Has to have a factor of degree 1 if reducible, as the sum of the degrees of the factors need to add up to 3, so either {1,1,1} or {2,1}. However, no such factor with deg 1 exists as $\sqrt[3]{2}$ is irrational. Thus, $x^3-2$ is irreducible, $⟨x^3-2⟩$ is maximal and $\mathbb{Q}[x]/⟨x^3-2⟩$ is a field.
3. ${\mathbb{F}}_2[x]/⟨x^3+x+1⟩$
   1. ${\mathbb{F}}_2[x]$ is clearly a field. We have it so ${\mathbb{F}}_2[x]\cong {\mathbb{Z}}_2$. This, plugging 0 in our function gives us 1, plugging 1 gives us 3=1. Either way there are no zeros, so no factors of deg 1 which is required and the polynomial is irreducible. By the same logic as the previous question, the ideal is maximal so this quotient ring is a field.
      We will come back to elements of these fields later.

Organization of $R[x]$ by classification of $R$

This started to get long so I made it into its own page: Organization of R polynomial x by classification of R