i.e. how elements really factor in $\mathbb{Z}[\sqrt{5}]$

Preliminaries

Fundamental theorem of Arithmetic:

Any number n>1 can be expressed as a product of primes, where the primes do not need to be distinct.

Rings:

A ring is just an Abelian Additive Group with Multiplicative Associativity and Distributive property. A commutative ring has multiplicative commutative property, a ring with identity or unity has the multiplicative identity (usually 1).

Ideals:

Similar to normal subgroups, ideals are subrings of rings s.t. $rI\subseteq I$ and $Ir\subseteq I$ for all r in the parent ring. Suppose you have some $x_1,...,x_k\in R$ then the following is also an ideal known as an ideal generated by $x_1,...,x_k$:

Note, we also have principle ideals that are ideals generated by a single element, ie for some element a

The trivial ideals (which are principal) are the 0 ideal and the entire ring $R$. These are expressed as:

A proper ideal $I$ of a commutative ring with unity is said to be prime if when $xy\in I$ for $x,y\in R$ either $x\in I$ or $y\in I$

Maximal ideals are the largest ideals of a ring, rigorously, if $I$ is a maximal ideal, for every $J$ ideal s.t. $I\subseteq J\subseteq R$ , then $J$ is either $R$ or $I$.

For any two ideals, the product is again an ideal. The product follows simple multiplication distributive rules (FOIL lmfao)

Integral Domain:

An integral domain is a commutative Ring (Abelian Additive Group with Multiplicative Associativity and Distributive property) with unity that meets the following condition:

If, $\mathrm{\forall }a,b\in R$ if $ab=0$ then either $a=0$ or $b=0$

Definitions within integral domains

Associates

Two elements, say $a,b\in D$ are associates if there exists $u\in D$ such that $a=ub$ where u is a unit.

Irreducible

An element, $c\in D$, is said to be irreducible if when c=ab, either a or b is an unit. Works in $\mathbb{Z}$ as we have units for A and B

Prime

An element, $p\in D$ is said to be prime if when p|ab then either p|a or p|b

note: Prime $\ne$ Irreducible. They can be the same but thats not always the case in every integral domain

Principle Ideal Domain (PID):

every ideal is a principle ideal.

Unique Factorization Domain (UFD):

A Unique Factorization Domain or UFD is where the Fundamental theorem of Arithmetic holds.

Any integral domain D is an UFD iff the following hold:

1. Let $a\in D$ such that $a\ne 0$ and a is not an unit. Then a can be written as a product of irreducible elements in D.
2. Let $a=p_1...p_r=q_1...q_s$ where the $p_i^{\prime }s$ and $q_i^{\prime }s$ are irreducible. Then r = s and there is a $\pi \in S_r$ (permutation in the cycle group of $S_r$) such that $p_i$ and $q_{\pi }(j)$ are associates for $j=1,...,r$. (Just a super fancy way of saying ever p is as associate of some q)

Note, $\mathbb{Z}$ is an UFD by the fundamental theorem of Arithmetic. Please observe the following:
30= (2)(3)(5) = (2)(-3)(-5)

We see that the first rule holds as 30 is not zero and not an unit in $\mathbb{Z}$. Additionally, 2, 3, 5 are irreducible as the only factors are themselves and 1, and 1 is an unit. Similarly, 2,-3,-5 have to have -1 as a factor, which is also a unit.
The second rule also holds, as firstly notice 2= (1)2, 3 = (-1)(-3), and 5 = (-1)(-5). as 1 and -1 are all in $\mathbb{Z}$, these are all associates.

$\mathbb{Z}[\sqrt{-5}]$

Lets dive deeper. $\mathbb{Z}[\sqrt{-5}]$ is an integral domain defined as:

Now notice, this fails the fundamental theorem of arithmetic as there are multiple irreducible factorizations but

However, all these elements are non-associate.

To understand this, lets define the norm function N:

Such that

For some general element $(a+b\sqrt{-5})\in \mathbb{Z}[\sqrt{-5}]$
Notice the following:

$\mathbb{Z}[\sqrt{-5}]$ is not a Principal Ideal Domain (PID):

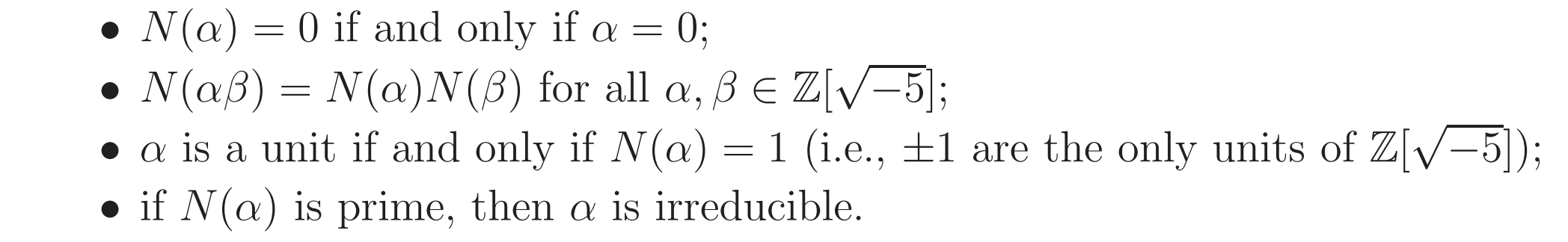
For example, take the ideal:

Now, if $I$ was principal then $I=<a>$. However, such for homework we proved $2$ and $1+\sqrt{-5}$ are irreducible. This the only common factors are 1, and we have it so a=1 or $I=<\pm 1>=\mathbb{Z}[\sqrt{-5}]$. because 1 will generate the entire ring. However, $3\in \mathbb{Z}[\sqrt{-5}]$, but $3\notin I$

Prime Ideal in $\mathbb{Z}[\sqrt{-5}]$

Take the ideal

We will show $I$ is infant a prime ideal.

First notice any element in $\mathbb{Z}[\sqrt{-5}]$ is only in $I$ if and only if the integers have the same polarity, ie let $\alpha$ be such an element:

If $\alpha \in I$ then it must be that:

Now, taking the middle equation, we can see the expansion:

Leaving us with the following two equations:

Now notice the following:

This $z_1,z_2$ have the same polarity (both odd or even)
In the opposite direction, notice:
case 1: both $z_1,z_2$ are even. Then is is easy as

The above works as $r_2$=0
Case 2: Both $z_1,z_2$ are odd:

Then notice, we can rework the equations above to state:

From here, it is clear that we have solutions for odd D and even C. Thus again $\alpha \in I$.

Now, we can show that $\mathbb{Z}[\sqrt{-5}]/I\cong \{0+I,1+I\}\cong {\mathbb{Z}}_2$ which is a field, thus $I$ is a maximal ideal and therefore prime.

Ideal Multiplication:

Ideal multiplication follows by simply multiplying the ideals. i.e.:

We wish to prove $<2,1+\sqrt{-5}{>}^2=<2>$ , we show this by showing they are subsets of each other.
now notice, we can rewrite all the elements as such:

Thus all the elements are divisible by 2 and therefor are also in $<2>$. This means

For the other direction we need to show $<2>\subseteq <2,1+\sqrt{-5}{>}^2$
Now notice,

And couple this with 2

Fundamental theorem of Ideal theory:

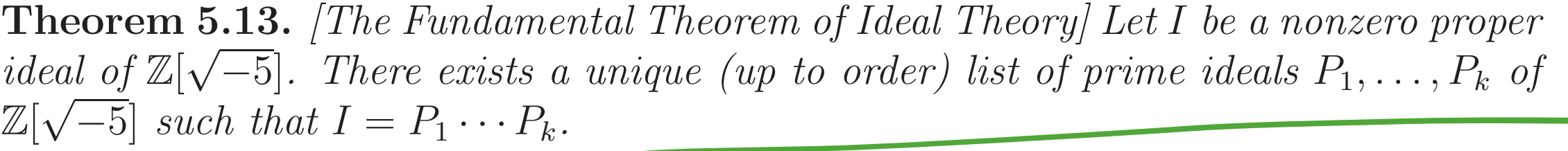
(Similar to the Fundamental theorem of Arithmetic)

Let $\alpha \in \mathbb{Z}[\sqrt{-5}]$ be a non-zero element. Then $\alpha$ is irreducible iff

1. $<\alpha >$ is a prime ideal in $\mathbb{Z}[\sqrt{-5}]$ (ie $\alpha$ is a prime element)
2. or $<\alpha >=P_1{P}_2$ where $P_1$ and $P_2$ are non-principal prime elements of $\mathbb{Z}[\sqrt{-5}]$