Question 0

Top

a:

A Ideal in a commutative ring $R$ with identity is a subring where for all $i$ in the ideal$\{ri\subset I\mid r\in R\}$.

b.

A group action on this map can be defined as $\mathrm{\Phi }(g,x)=gx$ for all $g\in G$ and $x\in X$.

Bottom

a.

A $H-coset$ in $G$ for some $g\in G$ is $gH=\{gh\mid \mathrm{\forall }h\in H\}$.

b.

For $\mathbb{Z}[i]$ the division algo can be formulated as the following:

For any $p(i),g(i)\in \mathbb{Z}[i]$ there exists $q(i)$ and $r(i)$ where

And $N(r(i))$ is less then $N(g(i))$ or is zero. Note the norm function here is $N(a+bi)=a^2+b^2$

For $\mathbb{Q}[i]$ the division algo can be formulated as the following:

For any $p(x),g(x)\in \mathbb{Q}[x]$ there exists $q(x)$ and $r(x)$ where

And the degree of $r(x)$ is less then $g(x)$ or is zero.

Question 1

Top

a.

$\mathbb{Q}=G$ and $\mathbb{Z}=H$. This will be proved again later.

b.

Proof:

1. Lets first prove $\mathbb{Q}(\sqrt{a}+\sqrt{b})\subset \mathbb{Q}(\sqrt{a})(\sqrt{b})$.
   1. This is easy as we have additive closure, so if both $\sqrt{a},\sqrt{b}$ are in $\mathbb{Q}(\sqrt{a})(\sqrt{b})$ we have it so $(\sqrt{a}+\sqrt{b})\in \mathbb{Q}(\sqrt{a})(\sqrt{b})$ and this direction is proved.
2. $\mathbb{Q}(\sqrt{a})(\sqrt{b})\subset \mathbb{Q}(\sqrt{a}+\sqrt{b})$
   1. We have to prove that $(\sqrt{a}),(\sqrt{b})\in \mathbb{Q}(\sqrt{a}+\sqrt{b})$
   2. Notice, $\frac{1}{\sqrt{a}+\sqrt{b}}=\sqrt{b}-\sqrt{a}\in \mathbb{Q}(\sqrt{a}+\sqrt{b})$.
   3. $\sqrt{a}+\sqrt{b}+\sqrt{b}-\sqrt{a}=2\sqrt{b}$ and similarly $\sqrt{a}+\sqrt{b}-(\sqrt{b}-\sqrt{a})=2\sqrt{a}$
   4. From here, we know $\frac{1}{2}\in \mathbb{Q}\in \mathbb{Q}(\sqrt{a}+\sqrt{b})$
   5. So, $\frac{1}{2}2\sqrt{b}=\sqrt{b}\in \mathbb{Q}(\sqrt{a}+\sqrt{b})$ and $\frac{1}{2}2\sqrt{a}=\sqrt{a}\in \mathbb{Q}(\sqrt{a}+\sqrt{b})$.

Bottom

a.

#fields

b.

The norm of $\mathbb{Z}[\sqrt{-5}]$ is defined as $N(a+b\sqrt{-5})=a^2+5b^2$. This exists in the natural numbers, and notice that $a^2$ or $b^2$ can never be negative. Thus all norms less then 5 have to be able to be written as a square of integers $a^2$. Both $\sqrt{2},\sqrt{3}\notin \mathbb{Z}$ and this norm is not possible.

Question 2

Top

a.

Proof:

1. Let $g\in G\setminus H$. and $h\in H$. We have to show $h\in ⟨G\setminus H⟩$.
2. First, lets see where $gh$ is. Notice that if $gh\in H$ then we would have $gh{h}^{-1}=g\in H$ which is a contradiction. So $gh\in G\setminus H\subset ⟨G\setminus H⟩$.
3. This is good because we know that $g$ and all its powers are also in $⟨G\setminus H⟩$. Thus $g^{-1}gh=h\in ⟨G\setminus H⟩$ and we have proved that we can generate every element of $H$ with $⟨G\setminus H⟩$.

b.

Proof:

1. For the sake of contradiction, assume that $\psi :\mathbb{Q}\to \mathbb{Z}$ was an injective homomorphism.
2. Then, let $\psi (1)=a$. As the homomorphism is injective, is the case only $\psi (0)=0$
3. Then, we know$$a=\psi (1)=\psi (\frac{1}{n}{)}_1+\psi (\frac{1}{n}{)}_2+....+\psi (\frac{1}{n}{)}_n=(\frac{a}{n}{)}_1+(\frac{a}{n}{)}_2+....+(\frac{a}{n}{)}_n\$\$.$$

Problem 2

Top

a.

#review

b.

The largest possible order in $S_8$ is the highest possible LCM with integers that add up to 8
This is $LCM(3,5)=15$ and are the elements that are the products of disjoin 3 and 5 cycles.

Problem 3

Top

a

g is power 4 as it gets the identity when multiplied to itself 4 times.

h is power 3

You can not use the LCM rule for the order here because that only works if the elemets commute. The order is infinate if you multiply it out

b

Proof:

1. The only subgroups of ${\mathbb{Z}}_p$ are trivial via langranges. So ${\mathbb{Z}}_p^{\star }$ can either be iso to {e} or ${\mathbb{Z}}_p$. ${\mathbb{Z}}_p^{\star }$ will always have $p-1$ elements, so the only case is that it is iso to $e$ which only happens when $p$ is $2$.

Bottom

a

Problem 4

Top

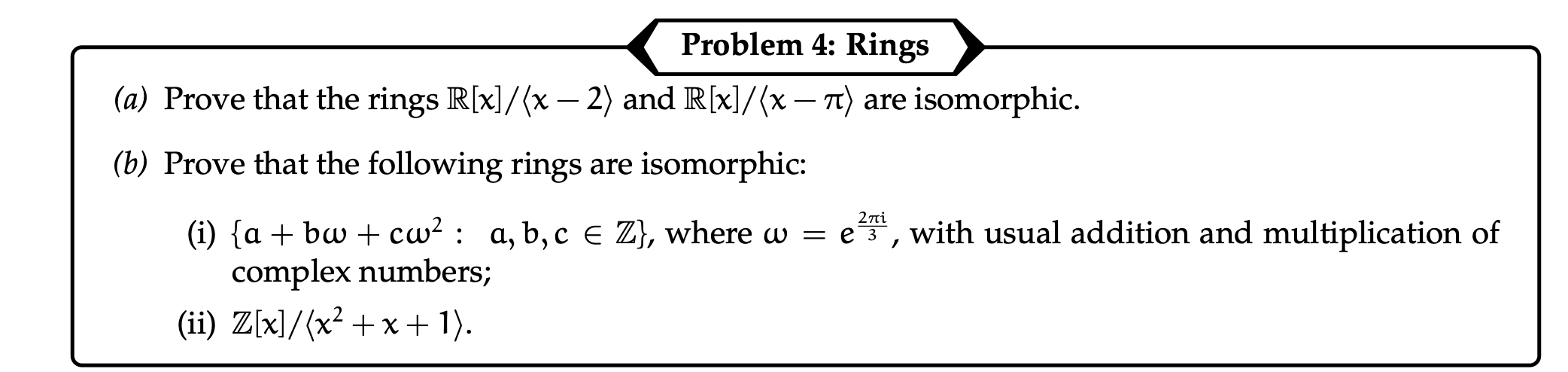
a

Lets define $\psi :\mathbb{R}[x]\to \mathbb{R}$ where $\psi (p(x))=p(2)$. The kernel of this is exactly $⟨x-2⟩$ as all these will go to zero when evaluated at 2, thus by first isomorphism theorem $\mathbb{R}[x]/Ker(\psi )=\mathbb{R}[x]/⟨x-2⟩$

Lets define $\psi :\mathbb{R}[x]\to \mathbb{R}$ where $\psi (p(x))=p(\pi )$. The kernel of this is exactly $⟨x-\pi ⟩$ as all these will go to zero when evaluated at $\pi$, thus by first isomorphism theorem $\mathbb{R}[x]/Ker(\psi )=\mathbb{R}[x]/⟨x-\pi ⟩$

Evaluation homomorphisms are surjective as the integers alone get every single real number $\mathbb{R}$

Bottom

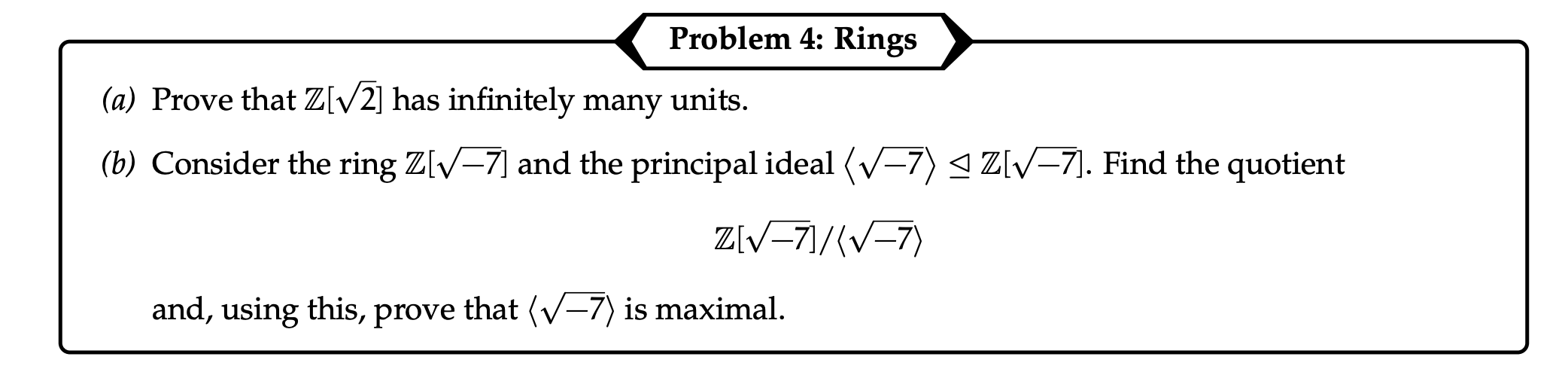
b.

Notice that the ideal $⟨\sqrt{-7}⟩$ contains elements

Then, you can get every element in $\mathbb{Z}[\sqrt{-7}]$ with integer multiples of 7.
Now notice, this leaves all integers such that
This leaves mod $0,1,2,3,4,5,6$ or more precisely has elements

This is just the ring ${\mathbb{Z}}_7$ which is a field as $7$ is prime. Thus we have it so $⟨\sqrt{-7}⟩$ is maximal.

Problem 6

c.

We know that $[L:K]=2$.

Letting $L=K[\sqrt{d}]$ we know that $[L:K]=2$ as the minimal polynomial is $(x^2-d)$

Now assume $d=c^2$ for some $c\in k$. then $L=K[\sqrt{d}]=K[c]$ and then as C is already in K we simply get $[K(c):K]=1$ which is a contradiction.

a.

We know $[\mathbb{Q}(\sqrt{3}):\mathbb{Q}]=2$ as the minimal polynomial in $\mathbb{Q}[x]$ is $x^2-3$.

By tower rule, another supposed subfield between $\mathbb{Q}$ and $\mathbb{Q}(\sqrt{3})$ would have to divide 2 in the natural numbers. However this is not possible as 2 is prime thus the only possible subfields are $\mathbb{Q}(\sqrt{3})$ and $\mathbb{Q}$.