Problem 0

0.1:

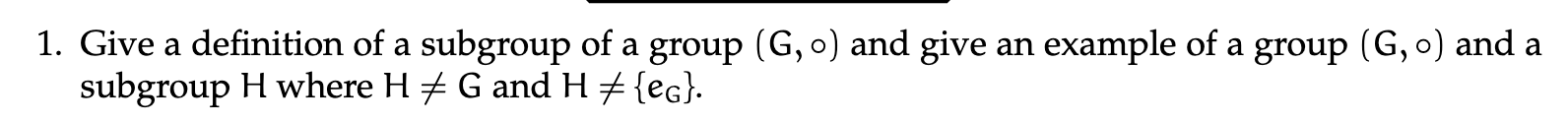
A subgroup is a subset which is a group under the same operation. This could be $\mathbb{Z}$ and $n\mathbb{Z}$.

0.2

Kernel of a homomorphism $\varphi :G_1\to G_2$ is all such elements where $\varphi (g)=0$ for $g\in G_1$. An example of this would be multiples of 5 in $\psi :\mathbb{Z}\to {\mathbb{Z}}_5$ def by $\psi (Z_1)=Z_2(mod5)$

Problem 1

1.1

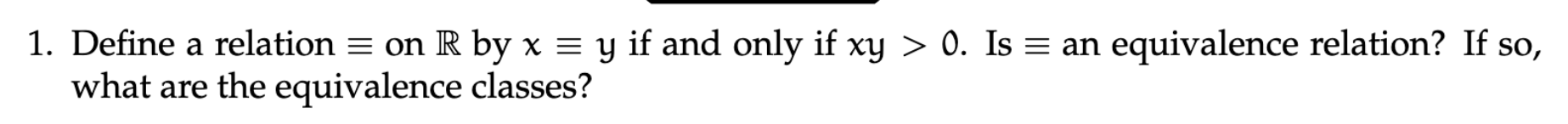
1. Reflexive: $x\equiv x$
   1. This fails, as if we let x be 0 then $00\ngtr 0$. Thus this is not an equivalence relation.

1.2

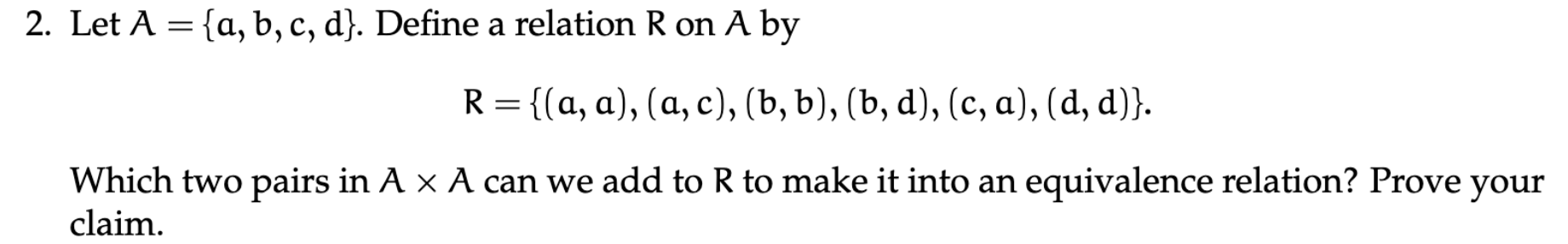
1. Reflectivity:
   1. $a\equiv a$, $b\equiv b$ , $d\equiv d$. However we do not have it so $c\equiv c$ so the first pair we need to add is $(c,c)$
2. Symmetry:
   1. $(a,c)⟹(c,a)$
   2. however, $(b,d)$ does not imply $(d,b)$ so this pair would also need to be added.
      We could check transitivity, however we found all the needed pairs. So I would add $(c,c)$ and $(d,b)$

Problem 2

2.1:

1. Stack notation:
   1. we have that the permutation takes the following:
      1. 1 -> 4
      2. 2 -> 7
      3. 3 -> 2
      4. 4 -> 1
      5. 5 -> 3
      6. 6 -> 8
      7. 7 -> 5
      8. 8 -> 6
   2. The cyclic notion is:
      1. (14)(2753)(68)
         1. remember disjointed cycles commute
   3. Order: LCM(2,4,2)=4.
   4. (12345678)(87654321)
      1. also just any disjointed permutations, (1234)(5678) as $S_8$ contains all elements from $S_{<8}$

2.2

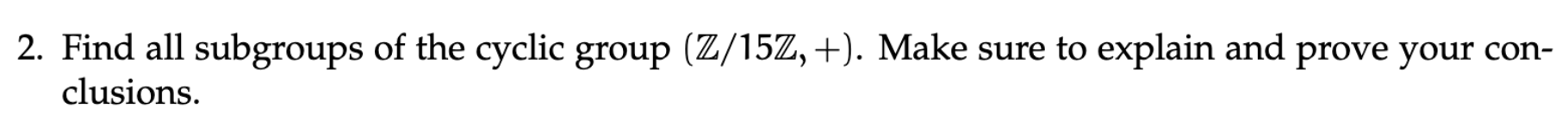
1. All subgroups if a cyclic subgroup are cyclic. So we are looking at :
   1. $⟨0⟩$,$⟨1⟩$,$⟨2⟩$,$⟨3⟩$,$⟨4⟩$,$⟨5⟩$,$⟨6⟩$,$⟨7⟩$,$⟨8⟩$,$⟨9⟩$,$⟨10⟩$,$⟨11⟩$,$⟨12⟩$,$⟨13⟩$,$⟨14⟩$
   2. Now some of these subgroups are the same, note:
      1. $⟨14⟩=\{14,13,12,11....\}=⟨1⟩$
   3. I want to use the same logic as in All Ideals in integers mod n to state that it is devisiors and every group goes down to the gcd, so here we have:
   4. $⟨0⟩,⟨1⟩,⟨3⟩,⟨5⟩$.
      1. Another way to think about this is the order of the subgroup must devide the parent group, which would make it only the following.

Problem 3

3.1

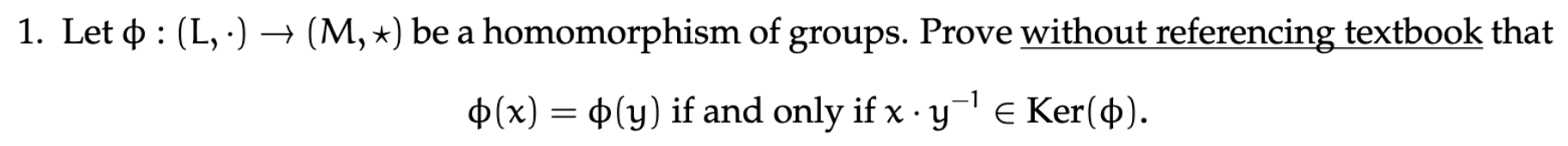
1. Proof:
   1. $\Rightarrow$ Assume:$$\varphi (x)=\varphi (y)$$
   2. Then notice:$$\varphi (x\cdot y^{-1})=\varphi (x)\star \varphi (y^{-1})=\varphi (y)\star \varphi (y^{-1})=\varphi (y\cdot y^{-1})=\varphi (id)=id$$
   3. $\Leftarrow$ In the other direction assume $x\cdot y^{-1}$ is in the Kernel. Then,$$\varphi (x\cdot y^{-1})=\varphi (x)\star \varphi (y^{-1})=\varphi (x)\star \varphi (y{)}^{-1}=id=\varphi (y)\star \varphi (y{)}^{-1}$$
   4. Specifically notice$$\varphi (x)\star \varphi (y{)}^{-1}=\varphi (y)\star \varphi (y{)}^{-1}$$
   5. By performing $\star \varphi (y)$ on the right we see that$$\varphi (x)=\varphi (y)$$
2. Given solution. Wrote it out because its kinda interesting:$$\varphi (x)=\varphi (y)⟺\varphi (x)\star \varphi (y{)}^{-1}=e_m⟺\varphi (x\cdot y^{-1})=e_m⟺x\cdot y^{-1}\in {\varphi }^{-1}(e_m)⟺x\cdot y^{-1}\in Ker\varphi$$

3.2

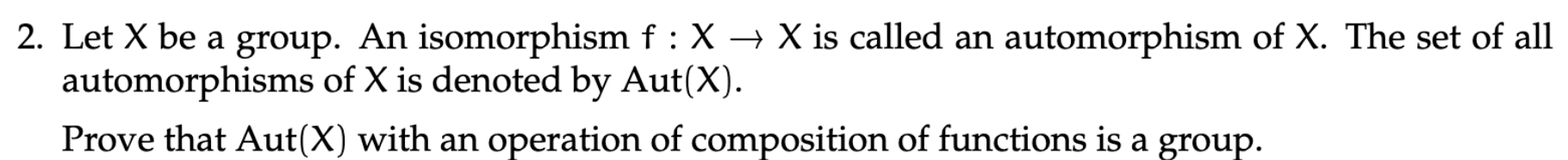
Things needed for a group:

1. Identity:
   1. Closure is met as you cannot go outside $X$ by definition
   2. Identity: Clearly, you can define an isomorphism $\varphi (x)=x$ thus this works as the identity as its homomorphic and bijective.
   3. Associativity: is met through the composition of functions, as composition of functions is associative.
   4. Inverse: By definition isomorphism are reversible, thus for any isomorphism $\psi$ we can define its inverse as ${\psi }^{-1}$.

3.3

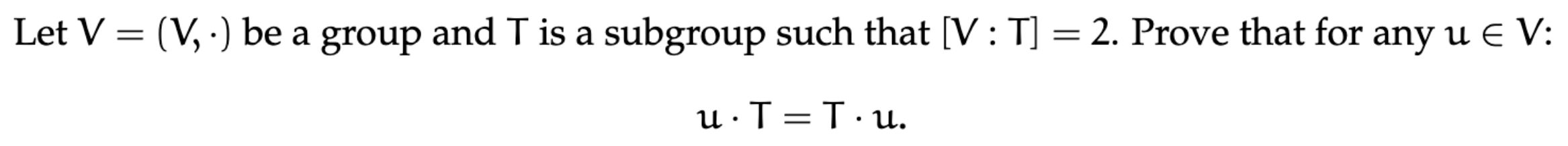
1. $[V:T]=2$ means there are 2 cosets of $T$ in $V$.
2. This means there are only two cosets that partition $V$, for $v,w\in V,\notin T$
   1. $e\cdot T$ and $v\cdot T$ for the left
   2. $T\cdot e$ and $T\cdot w$ for the right cosets.
3. as $e$ commutes, we know $e\cdot T=T\cdot e$. so it follows $v\cdot T=T\cdot w$ as this is the only other coset that can exist.