This book does not often go into the geometrics of vector spaces, ignoring 1A. Preliminaries and Introduction. For this, here is a quick guide on how to think about vectors geometrically. This mainly only works for vectors , or :
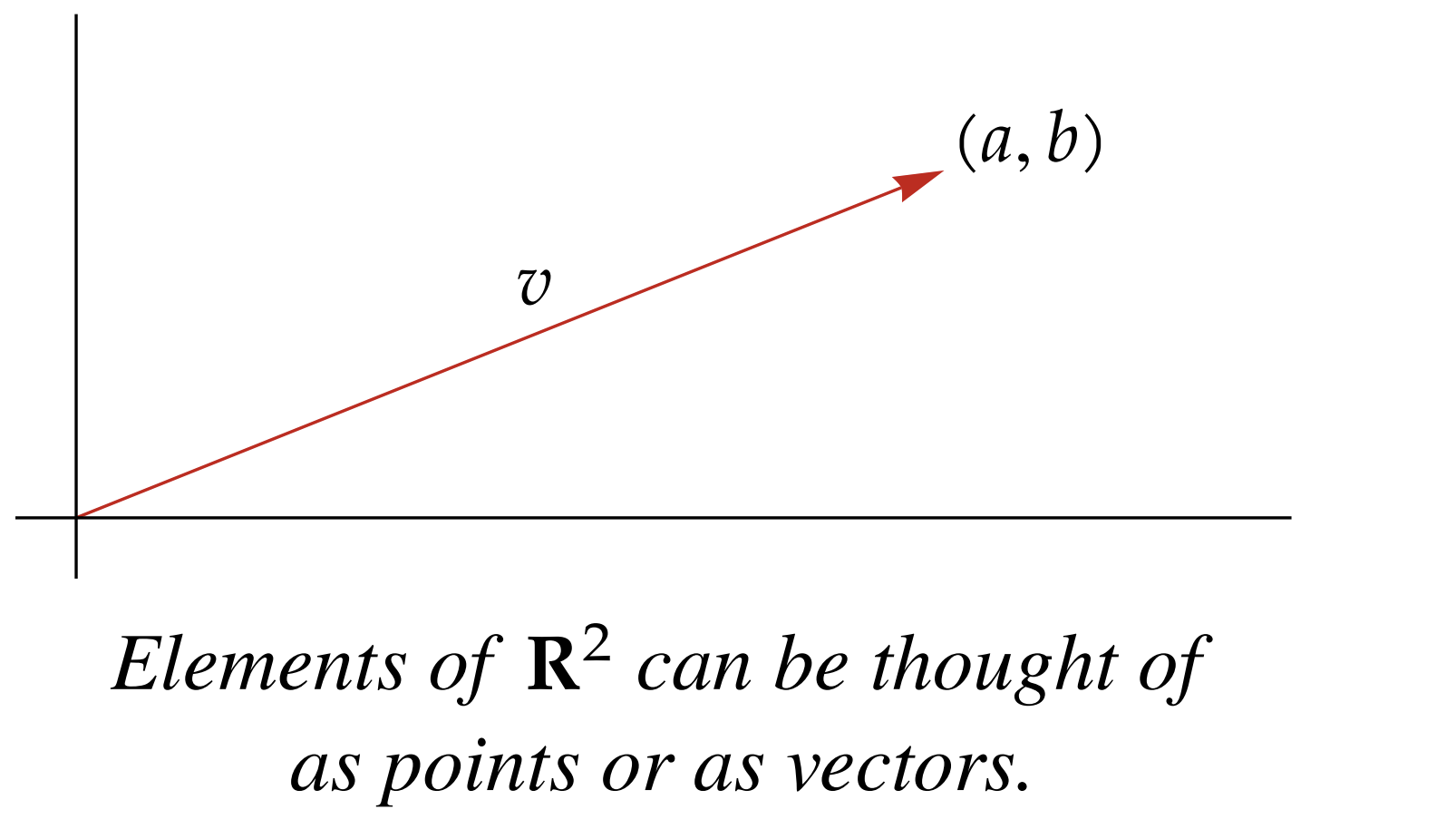
For some vector we can think of this as either a point or a vector:
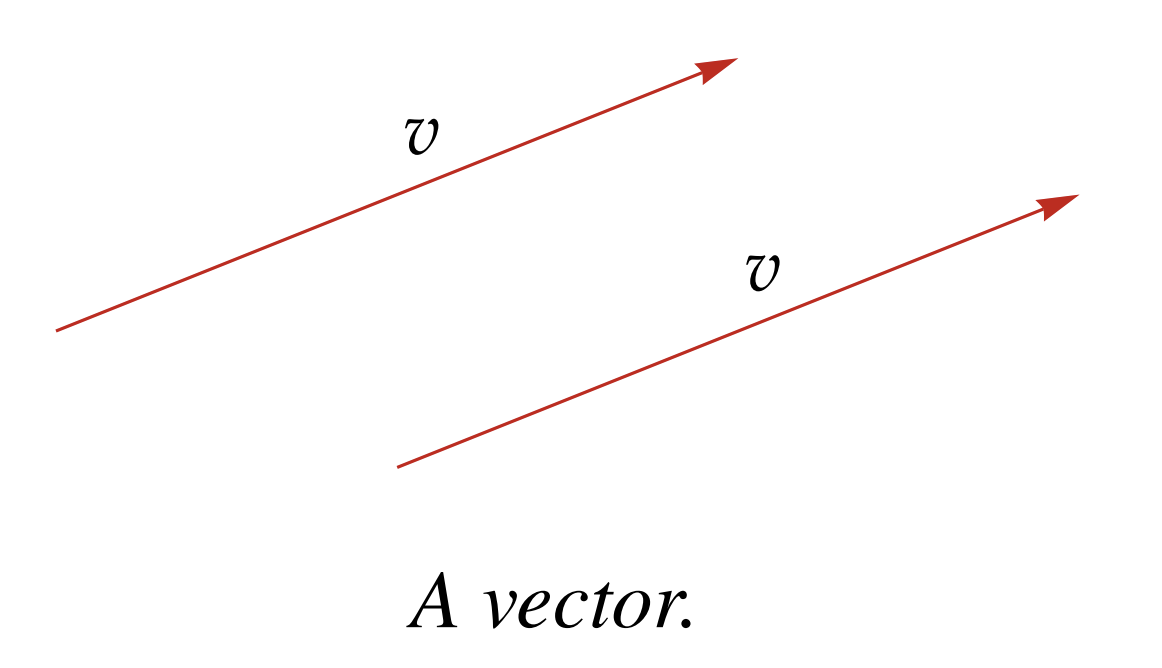
When thinking of it as an arrow we refer to it as a vector. Two vectors of the same length and direction are the same vector, even with different starting points:
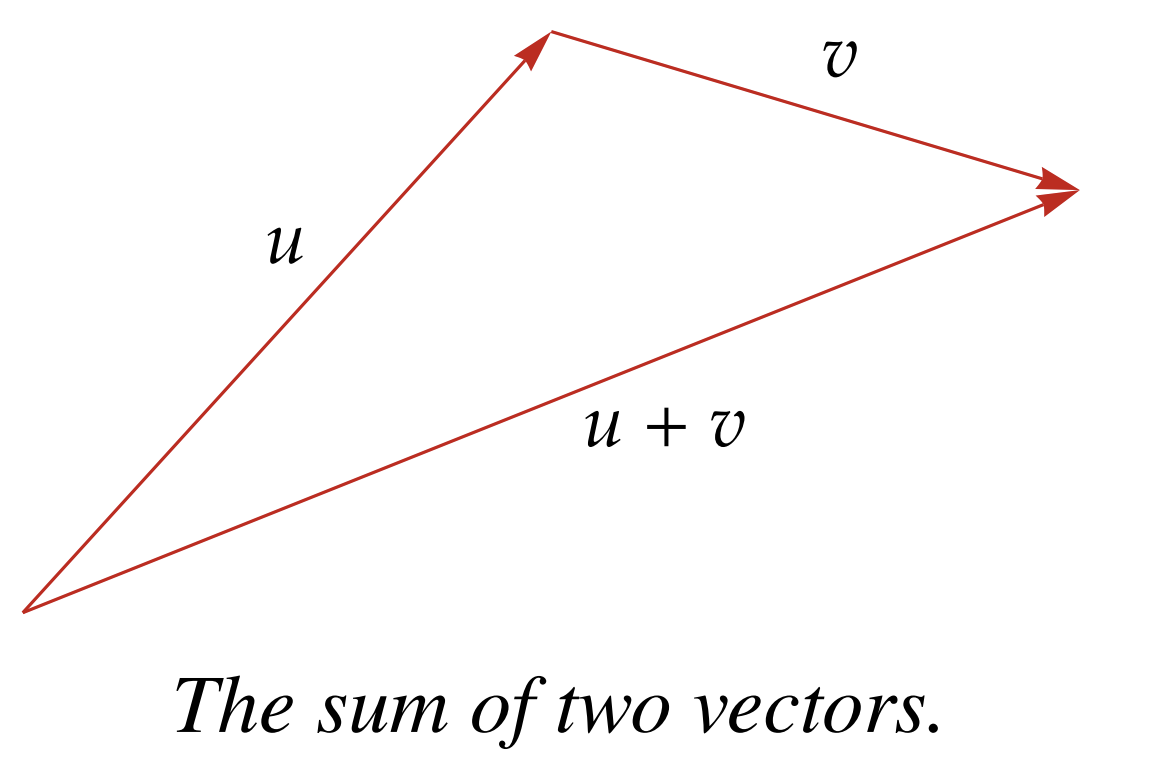
Addition makes sense geometrically, if you put the origin of the second vector at the endpoint of the first, you will end at the same endpoint as the sum vector:
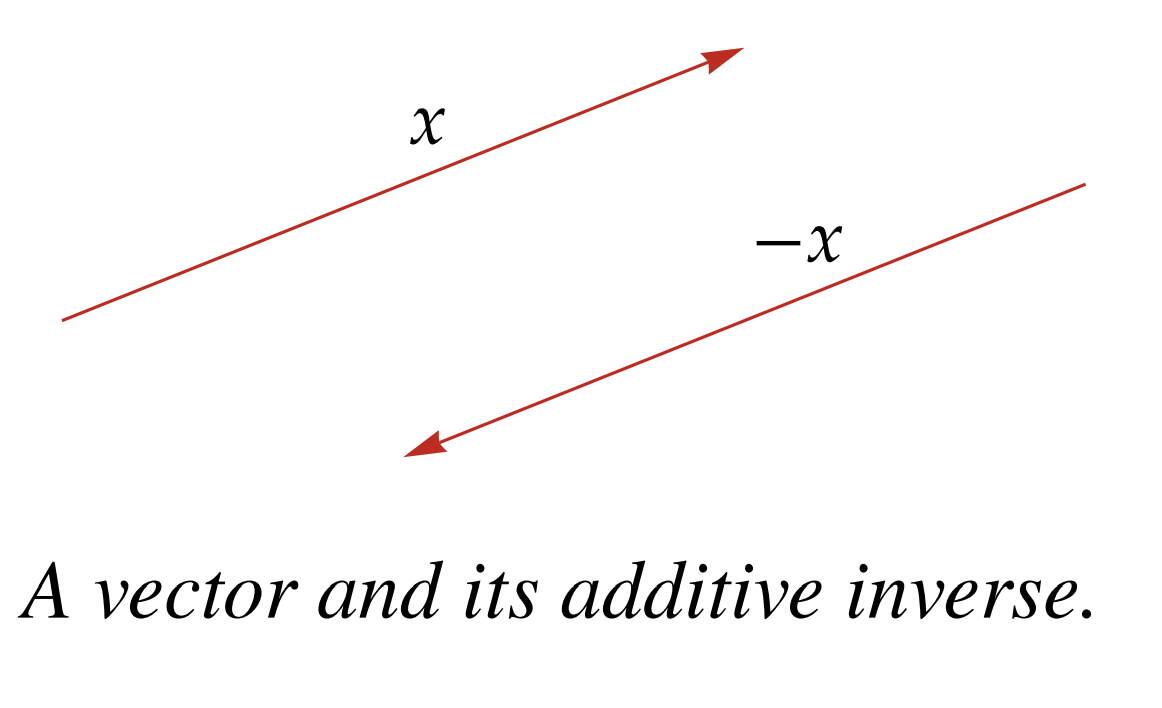
Likewise, additive inverses of vectors also make sense as they just have the opposite coordinates leading back to the origin:
Likewise scaler multiplication also has a nice geometric representation:
