Review questions:
 They are just their own objects with their own definitions. A vector space is something over a field with properties of addition, scalar multiplication, and distributive
They are just their own objects with their own definitions. A vector space is something over a field with properties of addition, scalar multiplication, and distributive

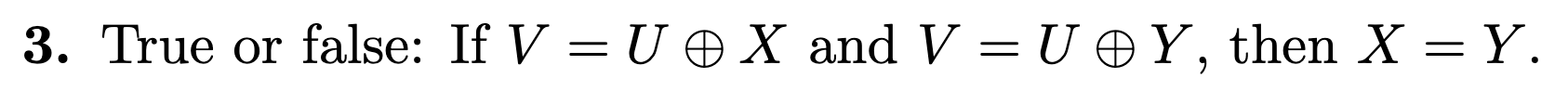 True, let have a basis and have basis . Then, by the proof of 2.33 in LADR, we know has basis .
True, let have a basis and have basis . Then, by the proof of 2.33 in LADR, we know has basis .
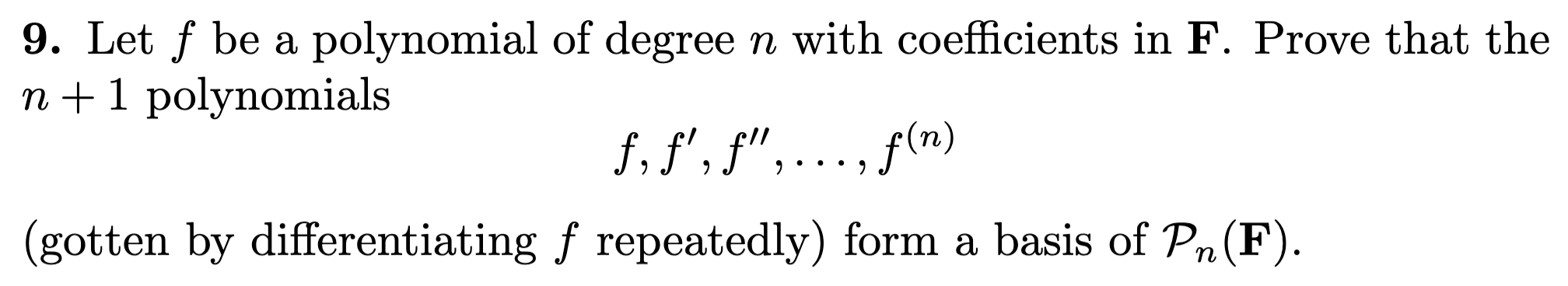 For this, first lets observe the standard basis for as
Now, as the dimension of both is we just have to prove linear independence or that it is a spanning list
We can easily prove independence as the only way to get the function is by setting all coefficients in each individual to 0. This is only possible if is written as the following linear combination:
Thus, it is linearly independent and a basis of
For this, first lets observe the standard basis for as
Now, as the dimension of both is we just have to prove linear independence or that it is a spanning list
We can easily prove independence as the only way to get the function is by setting all coefficients in each individual to 0. This is only possible if is written as the following linear combination:
Thus, it is linearly independent and a basis of
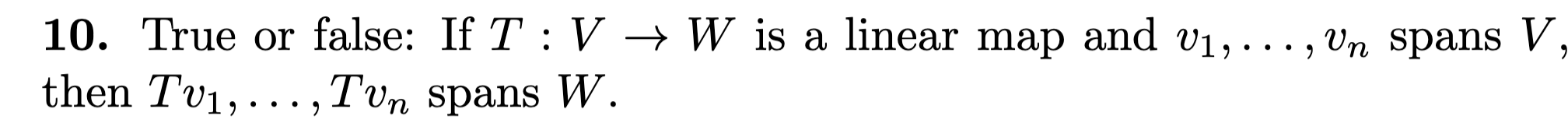 False, unless the map is surjective.
False, unless the map is surjective.
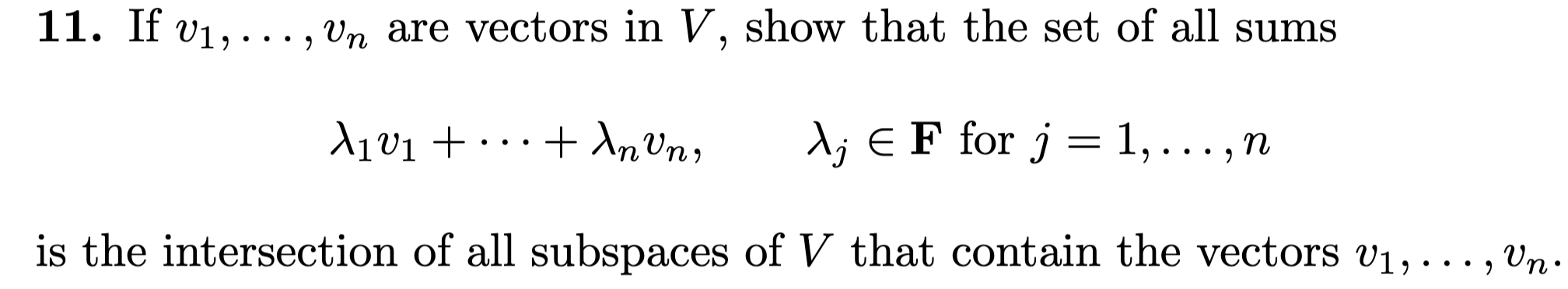
Through scaler multiplicative closure, each is in each subspace containing . With additive closure, the sum of all such with another scaler times a multiple is also within every subspace containing . thus, this must be in the intersection as scaler multiplicative and additive closure says the linear combination of is in every subspace containing .
 Yes, because otherwise all scaler multiplies including the missing vectors would be in . As we know this is not the case.
Yes, because otherwise all scaler multiplies including the missing vectors would be in . As we know this is not the case.
Homework 3A questions
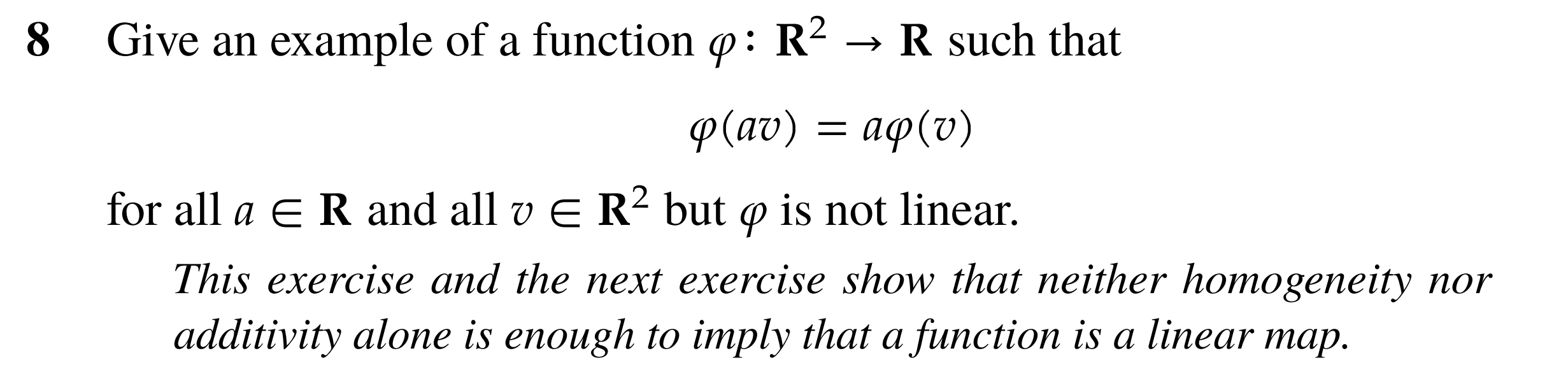
 This is the comp of functions. So starting slow, if we take any polinomial, and square it, then the map does not work. Take the two polynomials X and 1, letting . Then if we look at
This is the comp of functions. So starting slow, if we take any polinomial, and square it, then the map does not work. Take the two polynomials X and 1, letting . Then if we look at
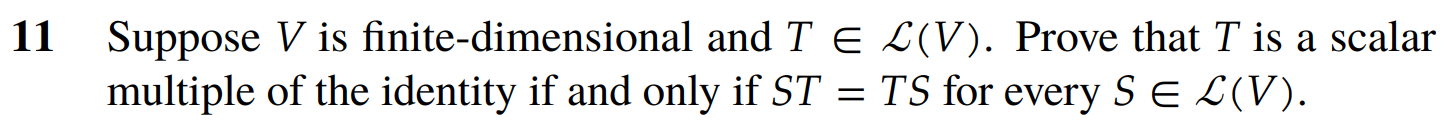 Proof:
Proof:
- is a scalar multiple of the identity for every
-
- Assume is a scalar multiple of the identity. Then, for some .
- Then we have it so that
- This holds due to definition 3.5
-
- Assume .
- Then,