Chapter 2 HW questions

2A

Question 2:

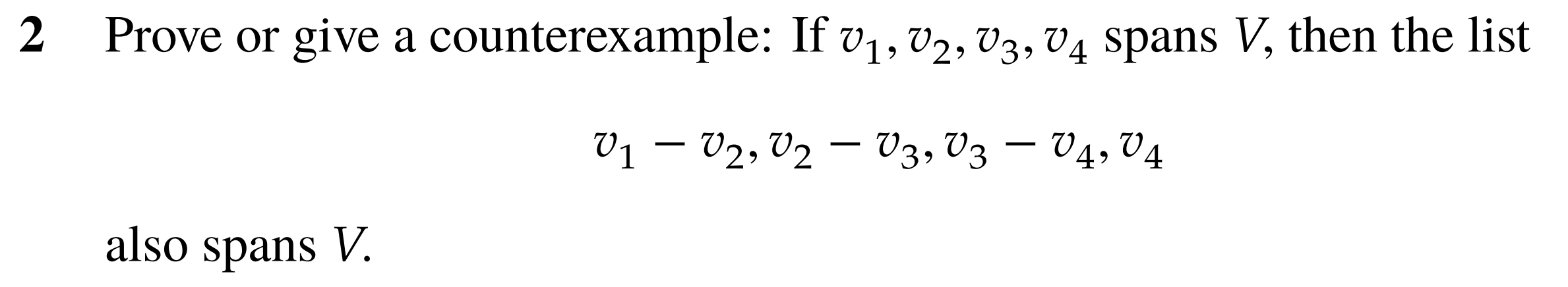Proof:

1. Let $u_1=(v_1-v_2),u_2=(v_2-v_3),u_3=(v_3-v_4),u_4=v_4$
2. Then notice
   1. $v_1=u_1+u_2+u_3+u_4=v_1-v_2+v_2-v_3+v_3-v_4+v_4=v_1$
   2. $v_2=u_2+u_3+u_4$
   3. $v_3=u_3+u_4$
   4. $v_4=u_4$
3. Thus yes, the list also spans $V$ because it can create the vectors of the original list. Through additive and scaler multiplicative closure, all the linear combinations must be in the list, showing that the span must be in the list.
4. Rigorously, for any $w\in V=\text{span}(v_1,v_2,v_3,v_4)$
5. $w=a_1{v}_1+a_2{v}_2+a_3{v}_3+a_4{v}_4=a_1(u_1+u_2+u_3+u_4)+a_2(u_2+u_3+u_4)+a_3(u_3+u_4)+a_4{u}_4$
6. This can be rewritten as: $a_1{u}_1+(a_1+a_2)u_2+(a_1+a_2+a_3)u_3+(a_1+a_2+a_3+a_4)u_4$
7. Finally substituting back the values for each $u_i$ we see $w=a_1(v_1-v_2)+(a_1+a_2)(v_2-v_3)+(a_1+a_2+a_3)(v_3-v_4)+(a_1+a_2+a_3+a_4)v_4$
8. Thus, any arbritary element in $V$ is also spanned by $v_1-v_2,v_2-v_3,v_3-v_4,v_4$

Question 3

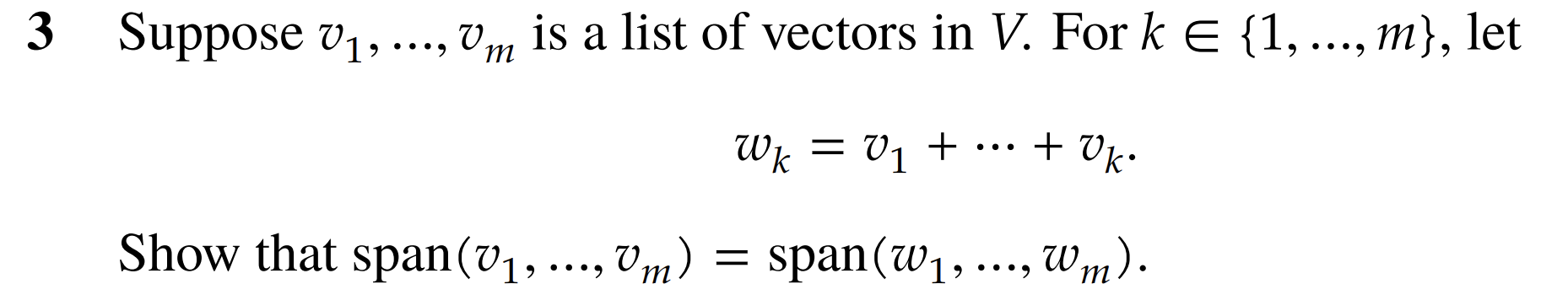Proof:

1. For any element $v_k$ notice that $v_k=w_k-w_{k-1}$. By this logic above we can easily see that $\text{span}(v_1,....,v_m)\subset \text{span}(w_1,.....,w_m)$ as every $v_k$ can be written as a linear combination of $w_1,...,w_m$ by setting the scaler in front of $w_k$ to $1$ and the scaler in front of $w_{k-1}$ to $-1$: $v_k=0w_1+....+(-1)w_{k-1}+1w_k+....+0w_m$
2. Similarly, its easy to see that $\text{span}(w_1,.....,w_m)\subset \text{span}(v_1,....,v_m)$ as each $w_k$ is a linear combination of $v_1,...,v_k$ so: $w_k=v_1+v_2+....+v_k+0v_{k+1}+.....+0vm$

Question 4

1. A list of length one in a vector space is linearly independent $⟺$ the vector in the list is not $0$
   1. A list of length one in a vector space is linearly independent $⟹$ the vector in the list is not $0$
      1. Assume the list $(v)$ with $v\in V$ is linearly independent. For the sake of contradiction assume $v=0$ Thus, we have it so $a_{1}v=0$ for $a_1\in F$
      2. Now notice, if $v=0$ then any possible $a_1\in F$ causes this equation to hold true. As we know $1\in F$, let $1v=0$ serve as our contradiction. As we assumed the list is linearly independent, this cannot be the case.
   2. A list of length one with a non zero vector in a vector space $⟹$ the list is linearly independent.
      1. consider the counterpos: the list is linearly dependent $⟹$ the element in the list is 0
         1. Assume the list is $v$, and we have it so $\lambda v=0$.
         2. As the list is dependent, we have it so lambda is not 0. Notice: $v=1v=({\lambda }^{-1}\lambda )v={\lambda }^{-1}(\lambda v)={\lambda }^{-1}0=0$
         3. thus, $v$ must be 0.
2. A list of length two in a vector space is linearly independent $⟺$ neither of the two vectors in the list is a scalar multiple of the other.
   1. A list of length two in a vector space is linearly independent $⟹$ neither of the two vectors in the list is a scalar multiple of the other.
      1. Assume that there is a list of length two in a vector space, and the list is linearly independent. For the sake of contradiction, assume that the two vectors are a scaler multiple of each other.
      2. Then, let the list be $v,av$ where $v\in V$ and $a\in F$
      3. Now notice the following equation: $b_{1}v+b_{2}av=0$ $b_1,b_2\in F$
      4. However, we can just set $b_1=-a,b_2=1$ and get the equation: $-av+(1)av=0$
      5. Clearly, this is a contradiction as we assumed that the list was linearly independent, meaning the only solution should be $b_1=b_2=0$
   2. A list of length two in a vector space is linearly independent $\Leftarrow$ neither of the two vectors in the list is a scalar multiple of the other.
      1. Consider the counter positive: A list of length two in a vector space is linearly dependent $⟹$ the two vectors in the list is a scalar multiple of the other.
         1. To prove the counter positive, take the list $v_1,v_2\in V$
         2. Writing out the linear combination for 0: $a_1{v}_1+a_2{v}_2=0$ $a_1,a_2\in F$
         3. As the list is linearly dependent, assume $a_1,a_2\ne 0$
         4. Then, we have it so: $a_1{v}_1=-a_2{v}_2$
         5. This implies: $v_1=\frac{a_2}{a_1}{v}_2$
         6. Proving that one has to be a scaler multiple of the other.

Question 7

1. Proof:

   1. Notice: $x(1+i)+y(1-i)=0$
   2. This provides the equation: $x+xi+y-yi=0$
   3. Which gives: $(x+y)+(x-y)i=0$
   4. The only way this holds is if $x+y=0$ and $x-y=0$
   5. This means $x=-y$ and $x=y$. The only case in which this holds in $\mathbb{R}$ is $x=y=-y=0$

2. Proof:

   1. As there are only two elements in the list, we need to show they are a scaler multiple of each other: $(1+i)=\frac{1+i}{1-i}(1-i)$
   2. done.

Question 11

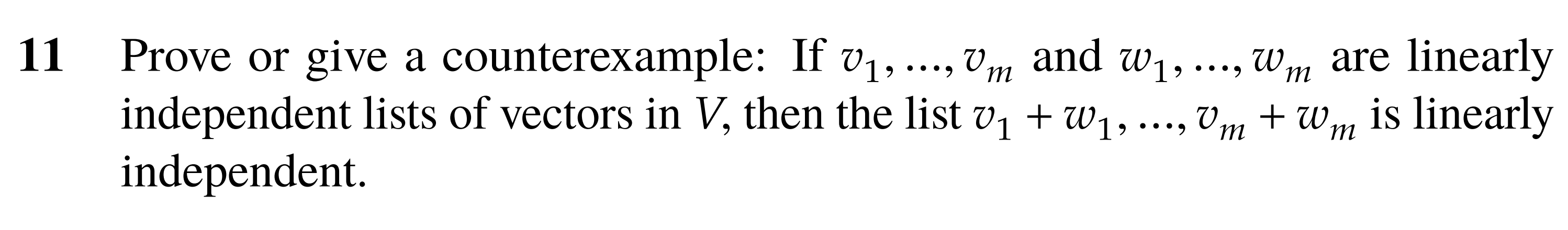
1. This is false, because a spanning list can also be linearly independent, however adding another linearly independent list makes it larger than the spanning list which is a clear contradiction.
2. Also lets take the list $v$ and $-v$. Both these lists are linearly independent (assuming $v\ne 0$. ) However, the list $v,-v$ is clearly dependent with both coefficients being 1

Question 15

A spanning list of ${\mathcal{P}}_4(F)$ is $1,x,x^2,x^3,x^4$. An independent list can not be larger than a spanning list. Thus the largest independent list can be of length 5.

Question 16

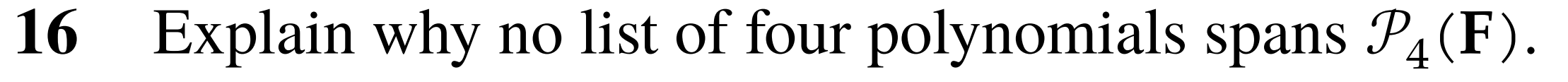Proof:

1. In ${\mathcal{P}}_4(F)$ $1,x,x^2,x^3,x^4$ is linearly independent. An independent list is always smaller than a spanning list, thus a spanning list can not have fewer than 5 vectors.

Question 17

Proof:

1. $V$ is infinite-dimensional $⟺$ there is a sequence $v_1,v_2,....$ of vectors in $V$ such that $v_1,....,v_m$ is linearly independent for every positive integer $m$
   1. $\Rightarrow$
      1. Assume $V$ is infinite-dimensional.
      2. Then there is no spanning set, thus there is an infinite
2. todo proof by induction

Question 18

Proof:

1. Lets create a list of independent vectors $v_1,v_2,...\in V$ such that for every $v_i$ there is a $1$ in the $i$th coordinate $(0,0,0,...,0,1,0,...)$.
2. This list is linearly independent, and infinitely long, thus any list spanning it would have to be longer than this list. Therefore, there is no list spanning it.