3C. Matricies

Skipping the definition of a matrix, this should be familiar to you

Linear Map Matrix

For any $T\in \mathcal{L}(V,W)$ where $v_1,v_2,...,v_n$ is the basis of $V$ and $w_1,w_2,...,w_m$ is the basis of $W$. The matrix of $T$ with respect to these basis is the $m$-by-$n$ matrix $\mathcal{M}(T)$ whose entries $A_{i,j}$ are defined by $T{v}_k=A_1,k{w}_1+....+A_m{w}_m$ If the basis are not clear from context, we use notation $\mathcal{M}(T,v_1,v_2,...,v_n,w_1,w_2,...,w_m)$

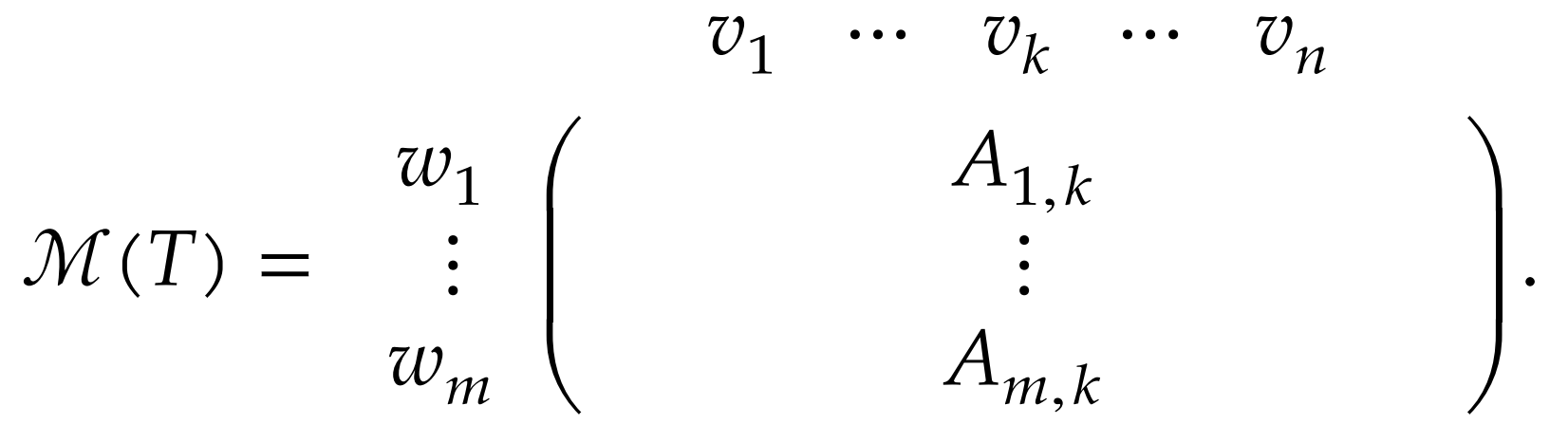
Did examples in notes

Addition

You add matrices by adding the respective element to each other.

Additionally, for $S,T\in \mathcal{L}(V,W)$ $\mathcal{M}(S+T)=\mathcal{M}(S)+\mathcal{M}(T)$

Similarly, scalar multiplication holds through functions too.

For example, for some $\lambda \in F$ and $T\in \mathcal{L}(V,W)$ $\mathcal{M}(\lambda T)=\lambda \mathcal{M}(T)$

Vector space

Matrices create a vector space.

Notation

The set of all $m$-by-$n$ matrices is denoted ${\mathbb{F}}^{m,n}$ with entries in $\mathbb{F}$

${\mathbb{F}}^{m,n}$ is a vector space over $\mathbb{F}$ with dimention

With addition and scaler multiplication defined above, ${\mathbb{F}}^{m,n}$ creates a vector space over $\mathbb{F}$ with dimension $mn$ Proof:

1. todo-weak prove that its a vector space over F
2. Dimension is easy, the basis of ${\mathbb{F}}^{m,n}$ as the set of matrices where only one element is $1$ and all other elements are $0$. There are $mn$ of such elements.

Matrix Multiplication

Created to make sure multiplication of linear maps holds. You take the row, column of the product and multiply the respective row and collum, with row from the first matrix and colum from the second. You can only multiply if the columns from the first match the rows from the second (inside numbers match.)

Stated more plainly:

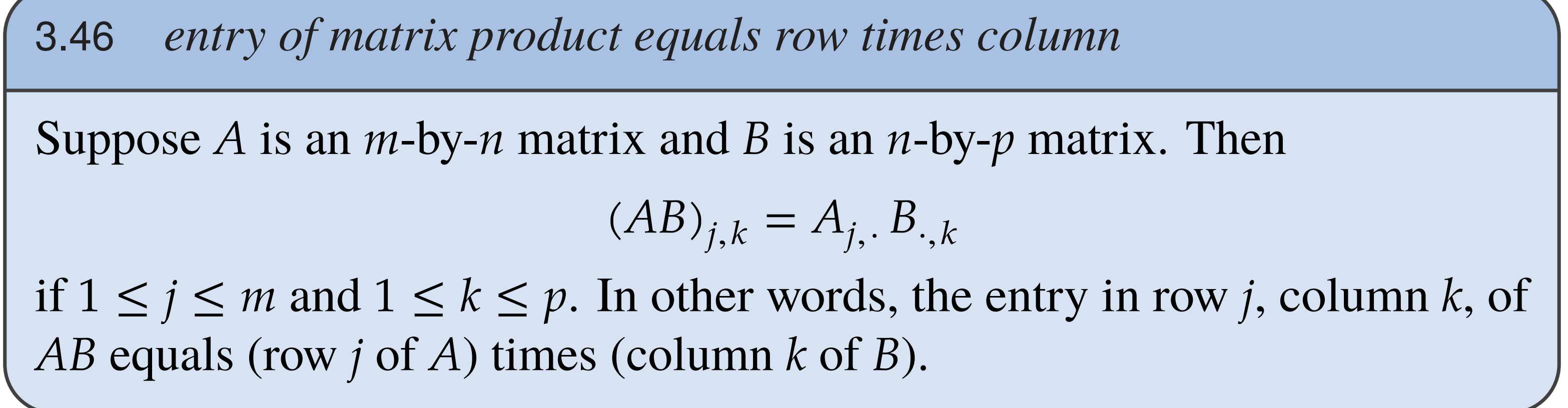
You can model multiplication of functions through multiplications of matricies. IE, $\mathcal{M}(ST)=\mathcal{M}(S)\mathcal{M}(T)$ #todo try and understand the motivation for this.

Row and column notation (similar to programming)

$A_{j,.}$ takes the $j$th row $A_{.,l}$ takes the $l$th column

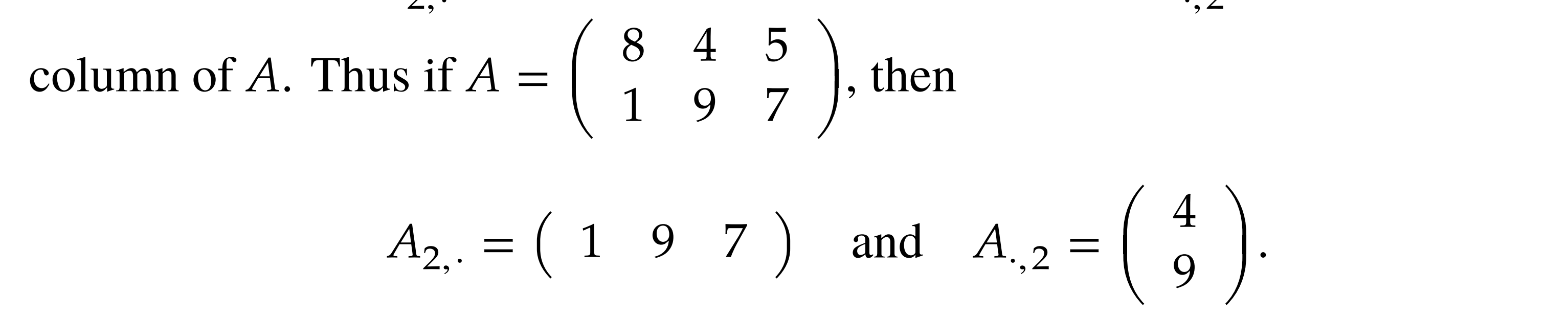
Column multiplication

$(AB{)}_{.,k}=A(B_{.,k})$ You can multiply the matrix times the column to get the column of the final matrix. Both have same number of rows

Additionally, if u are multiplying by a column matrix (n by 1), you can split up the elements and multiply each column separately.

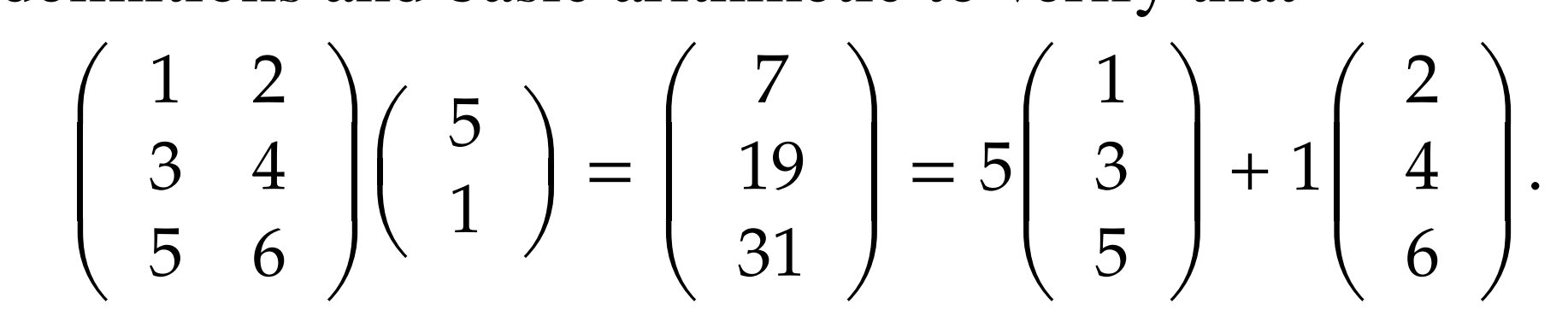
Similar results hold for the rows of a matrix.

todo What does this one mean?

#todo use the above statement to find the column and row rank of the following matrix. you can legit just take the span of the columns and rows btw. Also remember the dimension of the matrix to figure out how to get the right size dimension / basis. Like for rows, they can be max 2 in $F^{2,1}$

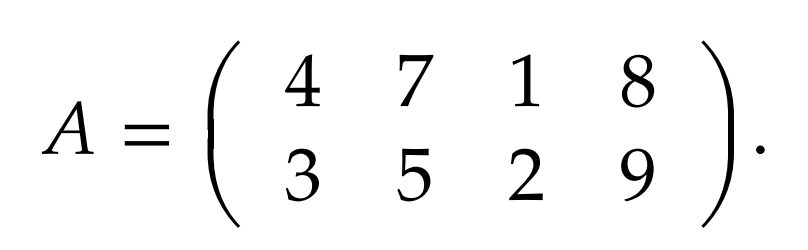
todo after solving the problem, why is it important for one to not be scalar multiple of another? does it show linear dependance in some way?

Transpose is taken by making every $A_{i,j}=A_{j,i}^T$. Additionally this means a $m$-by-$n$ matrix becomes an $n$-by-$m$ matrix.

Find the transpose of

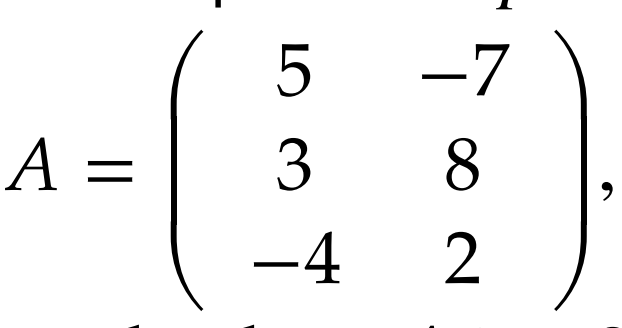
For all matrices column rank is the same as row rank. Complete the proofs to find out why todo (last 2 proofs) before def

Finally, we just denote rank

Rank Definition

The rank of a matrix is just the column rank of the matrix, i.e. the dimension of the span of the columns.