Homework 5

Chapter 3B Problems

2

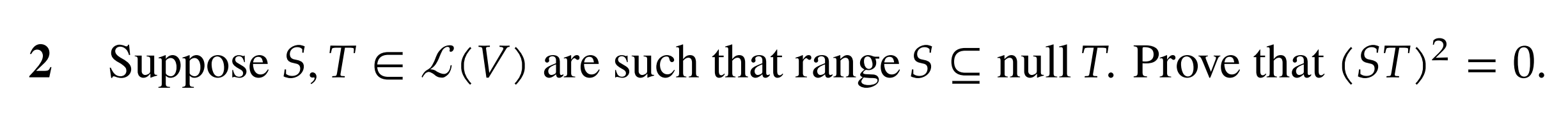
1. First notice that if we take $(ST)(ST)$, and label them as $(12)(34)$ where $1,3=S$ and $2,4=T$. Then, the element that goes through $3$ comes out in $\text{range }S$ which means it is also an element in $\text{null }T$, meaning after going through 2 it will be 0, and stay 0 thought the rest of the function as a linear map moves 0 to 0.

   In other words, for any element $v\in V$, we are moving the element with the following map: $v\to Tv\to STv\to TSTv\to STSTv$ Taking a closer look at $TSTv=T(ST)v$, meaning that the input $STv$ is always in $\text{range }S\subset \text{null }T$. Meaning that $TSTv=0$ and will stay 0 as any linear map moves identity to identity.

6.

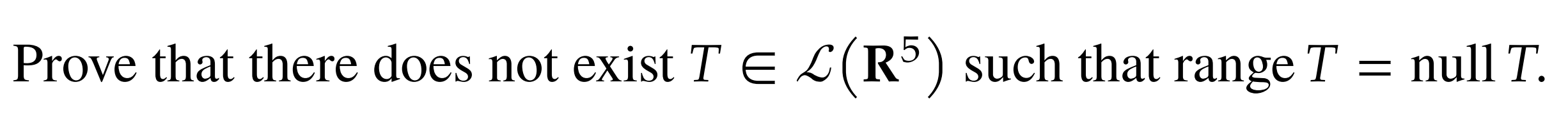
Notice that the fundamental theorem of linear maps states: $\text{dim }{R}^5=\text{dim range }T+\text{dim null }T$ As $\text{dim }{R}^5=5$, we have it so $\text{dim range }T=\text{dim null }T=2.5$, however, this is impossible in $R^5$.

check

7.

As $T$ is not injective, we know the null space of $T$ has to be greater than $0$. Now, notice that this means the null space has to be exactly 1, as if it was 2 or greater then the null space would be V itself. office-hours

11

Proof:

1. supose $(n_1,\dots ,n_k)$ be a basis of $\mathrm{null}T$. Extend to a basis of : $(n_1,\dots ,n_k,u_1,\dots ,u_m)$. Define $U=\mathrm{span}\{u_1,\dots ,u_m\}$.
2. then $V=\mathrm{null}T\oplus U$, hence $U\cap \mathrm{null}T=\{0\}$.
3. for all $v\in V$, write $v=n+u$ with $n\in \mathrm{null}T$, $u\in U$. then $Tv=Tn+Tu=0+Tu=Tu\in T(U)$, so $\mathrm{range}T\subseteq T(U)$.
4. then notice $T(U)\subseteq \mathrm{range}T$. thus $\mathrm{range}T=T(U)$ and $U\cap \mathrm{null}T=\{0\}$.

14

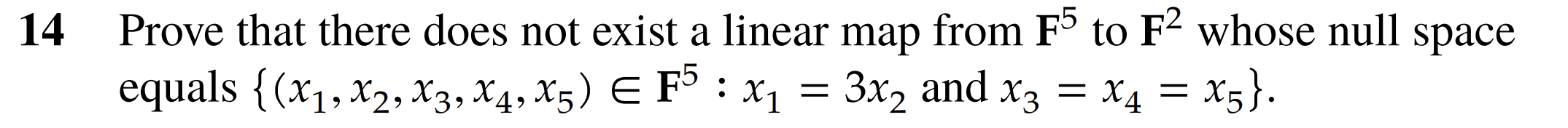Any element in this null space would look like $(3x_2,x_2,x_3,x_3,x_3)$ for each $x_i\in F$.

We know that the dim $F^5=5$ and dim $F^2=2$. Thus the max dimension of the range would have to be at most $2$. For the sake of contradiction assume such a map $T$ did exist, Then, by the fundamental theorem of linear maps $5\le \text{dim null }T+2$ $\text{dim null }T\ge 3$

then we know that the dimension of the null-space is at least 3. However, this null space is spanned by the vectors $(3a,a,0,0,0)$ and $(0,0,b,b,b)$ for $a,b\in F$ which is a basis; proving no such null space exists as this has a null space of dimension 2 which is a contradiction.

15

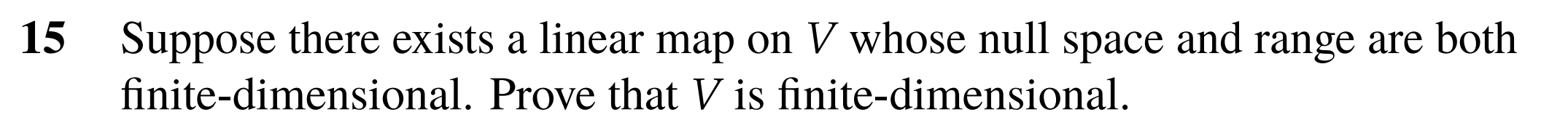Call the transformation T. From the fundamental theorem of linear maps we know $\text{dim }V=\text{dim range }T+\text{dim range }T$. By this we know that $\text{dim }V$ is finite dimensional, as $\text{dim range }T+\text{dim range }T<\infty$. #check The book specifies finite dimensional V

18

Proof:

1. $\Rightarrow$
   1. Assume $T\in \mathcal{L}(V,W)$ with $\text{null }T=U$.
   2. $\dim V=\dim (\text{null},T)+\dim (\text{range},T)=\dim U+\dim (\text{range},T)\le \dim U+\dim W.$
   3. $\Rightarrow \dim U\ge \dim V-\dim W.$
2. $\Leftarrow$
   1. Assume $\dim U\ge \dim V-\dim W$. Let $r=\dim V-\dim U\le \dim W$.
   2. Choose basis $u_1,\dots ,u_k$ of $U$; extend to basis of $V$: add $x_1,\dots ,x_r$
   3. Pick linearly independent $w_1,\dots ,w_r\subset W$.
   4. Define $T(u)=0$ for $u\in U,T(x_i)=w_i$ for $1\le i\le r$; extend linearly.
   5. Then $\text{null }T$

Chapter 3C Problems

1

This is true because at least $\text{dim range }T$ columns are linearly independent thus at least those columns are non-zero.

5

suppose $r=\text{dim range }T$.

1. Choose $v_1,....,v_r\in V$ so that for each $T{v}_i=w_i$ where $w_1,...,w_r$is a basis for $W$
2. We can extend this to a basis of $V$ by appending $u_1,....,u_{m-r}$.
3. Do the same thing in $W$ by setting each $w_k=T{v}_k$ and extending the basis
4. The matrix of this representation has all zeros accept for 1s in the diagonal rows and columns $1,...,r=\text{dim range }T$

6

1. If $T{v}_1=0$ then the first column of $\mathcal{M}(T)$ are all zero.
2. If $T{v}_1\ne 0$ then let $T{v}_1\ne w_1$ and extend it to a basis of $W$. This is only possible when you have a linear combination such that $w_1=1$ and everything else is $0$