Section 7

Sequences

A sequence is a function who’s domain is $\{n\in Z|n>=m\}$ where m is usually 0 or 1. Attaches each integer to that iteration of the sequence. Instead of $s(n)$ we usually write $s_n$.

We denote a sequence as $(s_n{)}_{n=m}^{\infty }$ for $\{s_m,s_{m+1},s_{m+2}\dots \}$. If the starting point is 1, we denote it as $(s_n{)}_{n\in \mathbb{N}}$. This makes sense as it is just the natural numbers 1 to inf.

Look at this example 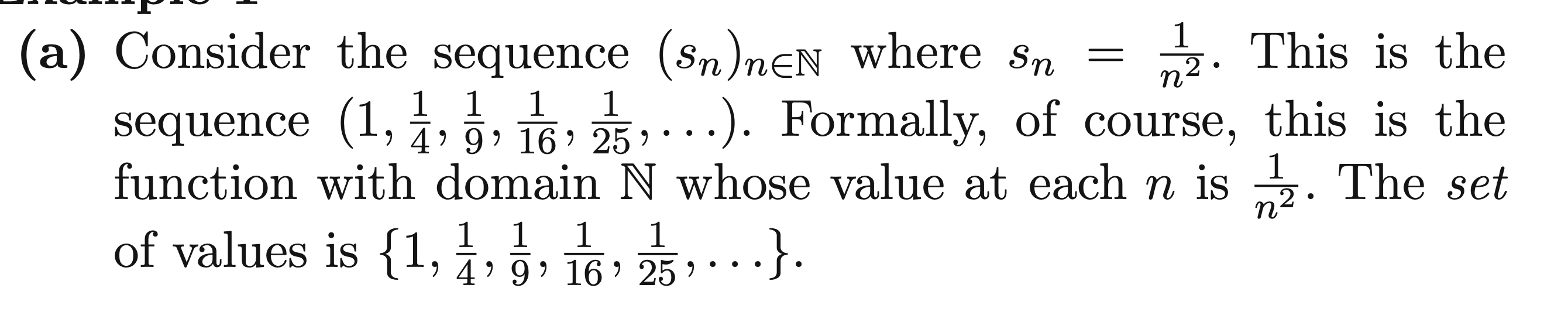We can essentially think of this sequence as $s(n)=\frac{1}{n^2}$.

Now it is important to denote differences between a sequence and its set of values. A sequence is its ordered output (such as a list and denoted as such too), while a set of values acts like a set (no order, no duplicate values, etc). Often, $s_n$ is ordered by $n\in \mathbb{N}$ in the order of $\mathbb{N}$.

Take a look at the example to view the difference:

Limit

The limit of a sequence $(s_n)$ is a real number that the values of $(s_n)$ are close to for all large $n$.

Definition of convergence

A sequence $s_n$ is set to converge to the real number $s$ provided that: For any $ϵ>0$ there exists a number $N$ such that $n>N⟹|s_n-s|<ϵ$ If we have it so $s_n$ converges to $s$, then we can sat ${\lim }_{n\to \infty }{s}_n=s$ or $s_n\to s$. $s$ is the limit of $s_n$. If some sequence does not converge it diverges.

Some books assume $N$ is a natural number. I like this. The last remark shows that you can always make $N$ into a natural number.

Another way tho think about it is, limit is the value that $s_n$ is close to or approaching for some very large $n$. Greater than $N$ is a formal way to say this, and $ϵ$ is a way to measure how close.

i.e. There exists such $N$ where if $n>N$ then the distance between $s_n$ and its convergence point $s$ is less than $ϵ$. This has to hold for any $ϵ$ giving us one convergence point and showing that as epsilon gets smaller this $N$ must still exist, however epsilon is never 0 so $s_n$ is never the exact same as $s$.

Before $N$ the sequence can be really far away from its convergence, but after $N$ we need some control and the sequence should be less than $ϵ$ away.

$N$ will have to be large for some small $ϵ$. This makes sense, as the further you are in the sequence the closer you get to the convergence point, reducing the distance or $ϵ$,

This means, usually, that if you pick a smaller $ϵ$ you need a larger $N$ because then the distance between $s_n$ and its limit $s$ is reduced with a larger $ϵ$.

You can also pick multiple $N$ for one epsilon. For example, take the sequence $s_n=\frac{1}{n^2}$. Then, suppose I pick $ϵ$ to be $\frac{1}{100}$ or $0.01$. Then, we know that $N=10$ works for this case, but $N=\{11,12,13,14\dots \}$ also work for this case. $N$ can always be replaced by a larger number, so if $N$ works $N+1$ also works. This is because $n>N⟹n>N+1$.

We usually only care about and use a very small positive $ϵ$. We want the sequence to be extremely close to the limit.

Infinite number of statements satisfy this condition, one for every $ϵ>0$, so it can be satisfied for $ϵ=\{0.1,0.01,0.001,0.0001,0.00001,\dots \}$.

Usually you can find a common $N$ for two sequences.

Limits are unique:

if $\lim s_n=s$ and $\lim s_n=t$ then we have it so $s=t$.

todo understand this proof more. Also in hw 2 and end of video 3.

Last property from video 3

If $s_n\to s$ and you change finitely many $b_n=a_n$ ($b_n$ is just $a_n$ with some finitely many terms change), we still have it so $b_n\to n$

This is because we can always find an $N$ after the last changed $b_n$ such that $b_n=a_n$. Then the limit definition is applied.

Essentially, if you change finitely many elements in a sequence, the limit does not change.