Section 4

The completeness axiom

This is the axiom that guarantees that $\mathbb{R}$ has no gaps.

Some really elementary proofs. Here is a rigorous definition of min and max: Apart from that, remember [ is inclusive and ( is exclusive. Here is the given definition:

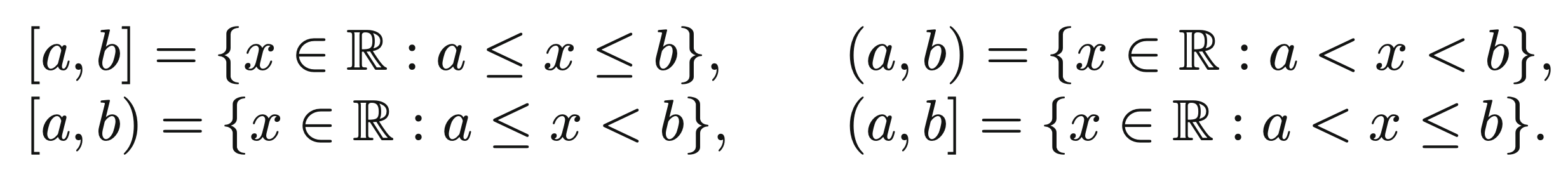
From here, notice that min$[a,b]$ is $a$ and max$[a,b]$ is $b$. $(a,b)$ has no min and no max. $[a,b)$ has a min $a$ but no max.

Remember, through an introductory proof we know that $\sqrt{2}$ is not rational. Thus we can say the following set has no max, but does have a min: 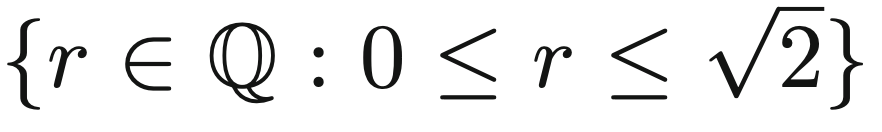Where min is 0, but there is no max.

Apart from this, $\mathbb{Z}$ and $\mathbb{Q}$ have no max or min. $\mathbb{N}$ has a min of $0$

Essentially, a set is bounded above if all elements within it are less than or equal to some real number $M$ Similarly, a set is bounded bellow if all elements within it are greater than or equal to some real number $m$ Note, these are not mins and maxes as they do not need to be within the set. A set bounded from above and below is said to be bounded

A set is automatically bounded by its min and max if they do exist.

To set the differences in more throughly, unlike min and max, for the set $(a,b)$ we have it so $a$ and $b$ are lower and upper bounds. Similarly, $a-1$ is also a lower bound and $b+1$ is also an upper bound. However, $b$ is the smallest upper bound and $a$ is the greatest lower bound.

Going back to a previous set 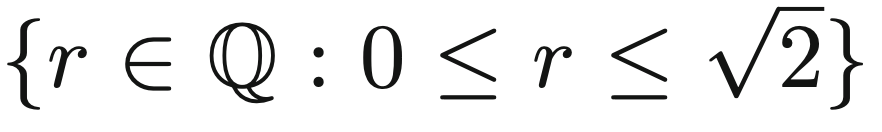notice that although $\sqrt{2}$ is not a max, it is an upper bound. It is also the least upper bound.

Supremum and infimum

Supremum is the least upper bound, while infimum is the greatest lower bound.

We denote these by $\text{sup }S$ and $\text{inf }S$ Unlike $\text{max }S$ and $\text{min }S$, $\text{sup }S$ and $\text{inf }S$ does not need to be within the set. A set can have at most one of each (they are unique if they exist, no multiple maxes or infimums) Likewise, if the max exists it is always a supremum. If a min exists it is always in infemum.

An important result from this and a combination of the statement on upper bounds of $(a,b)=b$ is that it is the least upper bound. Thus: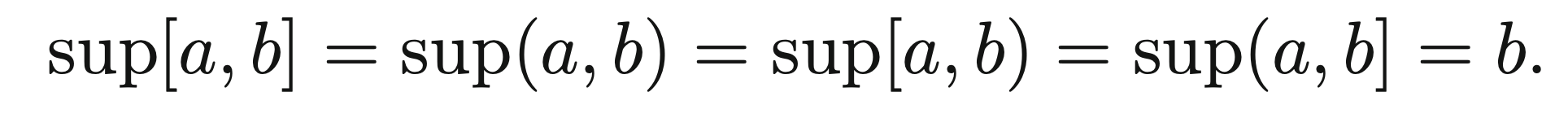

The following condition is useful for proofs: 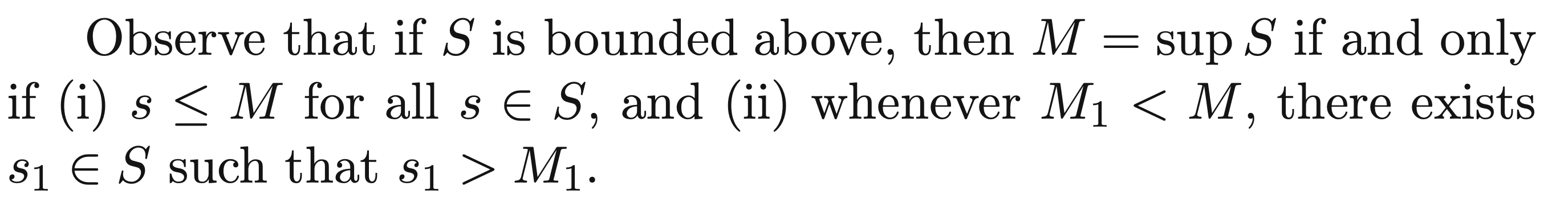Essentially, some M is a supremum of S if and only if it is an upper bound and any other $M_1$ less than $M$ is not an upper bound.

Completeness axiom

If there is an upper bound, as there are no gaps in $\mathbb{R}$, there exists a real supremum.

Formally: 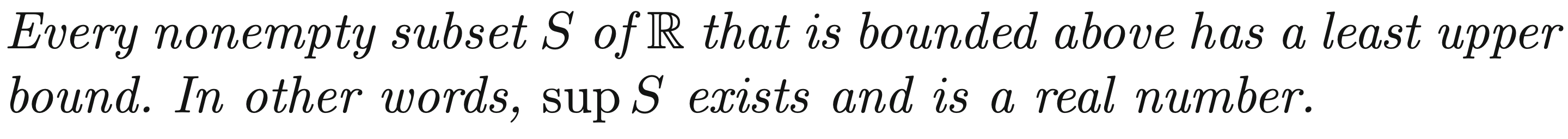also works for infimum.

It is important to note that this only work in $\mathbb{R}$ because there are no gaps. To see this take a look at the set $A=\{r\in \mathbb{Q}\mid 0\le r\le \sqrt{2}\}$. Now note, $\sqrt{2}$ is an upper bound, but it is not in $\mathbb{Q}$. Similarly, $\frac{3}{2}$ is an upper bound, however there are infniately many rational points between $\sqrt{2}$ and $\frac{3}{2}$. Thus there is no rational inf.

Archimedean Property:

For any $a>0$ and $b>0$, $\exists n$ such that $an>b$

todo look at the proof for this later

Denseness of $\mathbb{Q}$

There is always a rational number between any two non-equal real points.

todo I think there is a proof of this online too which i want to look at before.

todo also look at the exersizes look fire.

todo the questions from this section are extremely important for section 5