Section 14

Separate from book notes

Series essentially adds up the terms of a limit. It is important to note that the limit of a sequence is not the same thing as the sum of a series. For example $\lim \frac{1}{2^n}=0$ However ${\sum }_{n=1}^{\infty }\frac{1}{2^n}=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots =1$

For a sequence $s_n$ we can define the sum with elements of $s_n$ as the terms with ${\sum }_{k=1}^{\infty }{s}_k$ And it works backwards too, where you can consider the terms of a sum as its own sequence.

$(s_n)$ is the sequence of partial sums of the series, as defined bellow. It is not just the terms of the series.

We can consider the sequence of partial sums, which is sequence $(s_n)$ defined bellow $(s_n)=({\sum }_{k=1}^n{a}_k{)}_n^{\infty }$ Basiclly the $n$ th element in the sequence of partial sums is the sum of the first $n$ terms in the sum.

For ${\sum }_{k=1}^{\infty }k=1+2+3+4+5+\dots$ the sequence of partial sums would be $(1,3,6,10,\dots )$. Each element is called a partial sum.

A series converges to $s$ if its sequence of partial sums $s_n$ also converges to $s$. Likewise, if $s_n$ is bounded or monotone, the series is also bounded or monotone.

From the book

Continuing where we left off

Fortheremore we say a series $\sum a_n$ is meaning full only if it converges or goes to an inifinity. Else we define it as meaningless.

If all the terms $a_n$ of the series $\sum a_n$ are non-negative, then the sequence of partial sums $s_n$ is an increasing sequence. Thus, from the last few chapters, this either is bounded and coverges to the supremum or goes to $\infty$. Because of this $\sum |a_n|$ is always meaningful, and we say $\sum a_n$ converges absolutely if $\sum |a_n|$ converges. Absalutely convergent series are convergent.

Geometric series and P series in the book

To note, both are going from $n$ to $\infty$

For geometric series ${\sum }_{n=0}^{\infty }a(r{)}^n=\frac{a}{1-r}⟺|r|<1$

For p series ${\sum }_{n=1}^{\infty }\frac{1}{n^p}$ converges $⟺$ $p>1$.

For any series, if the sequence of partial sums is cauchy, i.e for any $ϵ>0\exists N$ where $n,m>N⟹|s_n-s_m|<ϵ$ then the series is cauchy.

Important

A series converges $⟺$ it is cauchy Similar to sequences

Additionally, If a series $\sum a_n$ converges, then $\lim a_n=0$

So if you can prove that the limit of $a_n$ not zero, then you know it does not converge.

Comparison test:

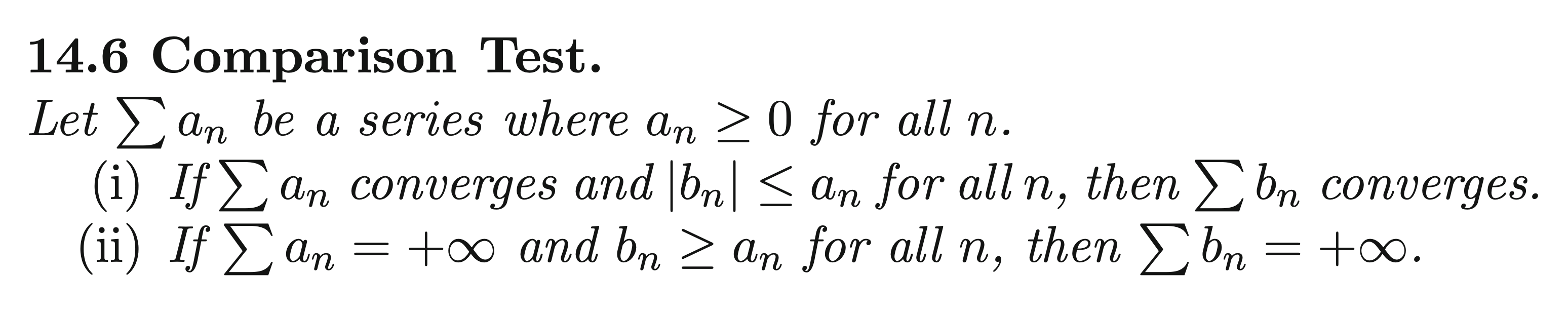
Important

Absolutely convergent series are convergent.

Essentially, if $\sum |a_n|$ converges then $\sum a_n$ converges.

Ratio test

Given a series $\sum a_n$ of non-zero terms

1. Converges absolutely if $\lim \sup |\frac{a_{n+1}}{a_n}|<1$
2. Diverges if $\lim \inf |\frac{a_{n+1}}{a_n}|>1$
3. Gives no information for other cases.

Root Test

This one is recommended Let $\sum a_n$ be a series and let $\alpha =\lim \sup |a_n{|}^{1/n}$

1. Then $\sum a_n$ converges absolutely if $\alpha <1$
2. Diverges if $\alpha >1$
3. If $a=1$ test is useless.