Standing and new assumptions:
- denotes either . Please note, sometimes we will just use
- all denote vector spaces over
Definition of Linear map
A linear map or linear transform is a function between two vector spaces that preserves addition and homogeneity:
- Addition: for
- Homogeneity: for
Homogeneity is a lot like preserving scaler multiplication. For linear maps we could use either notation, usual function notation or just
Through back from group theory:
Notation
- We denote the set of linear maps from to as
- The set of linear maps from to is denoted as
Examples:
Prove that the following are linear maps:
- Zero
- Zero is the function that is defined by taking every element to 0. I.E:
- To prove this is a linear map lets prove it preserves addition and homogeneity:
- Addition
- Let . Then:
- To help out I labeled which set 0 is in or if its the function. This will be assumed from now on.
- Homogeneity:
- Let
- Addition
- Identity operator
- By definition, the identity operator is a function such that
- Addition
- Homogeneity
- By definition, the identity operator is a function such that
- Integration
- Integration as a function in defined as
- is a function because when you add you just move the int to each part, and if u multiply by a scaler you can take it out of the integration.
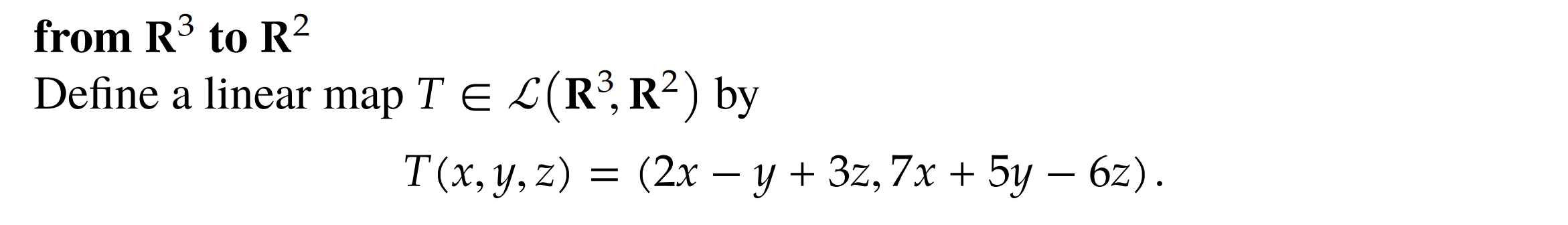
- For this last example, lets prove its a linear map.
- Let
- Addition:
- From the other side:
- Homogeneity:
- I will skip this proof for now.
- Addition:
- Let
- For this last example, lets prove its a linear map.
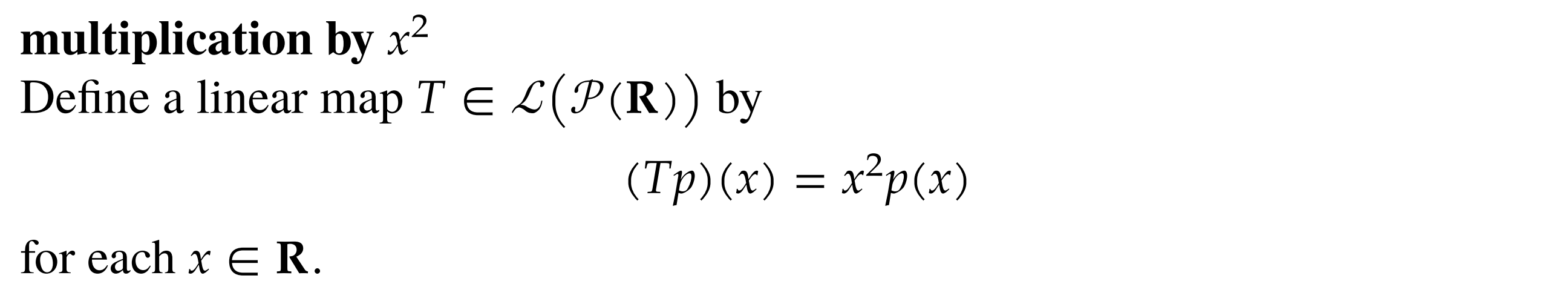
- This is a linear map as the following properties hold:
- Addition
- Let . Then notice:
- Let . Then notice:
- Homogenity:
- Let and .
- Then:
- Addition
- This is a linear map as the following properties hold:
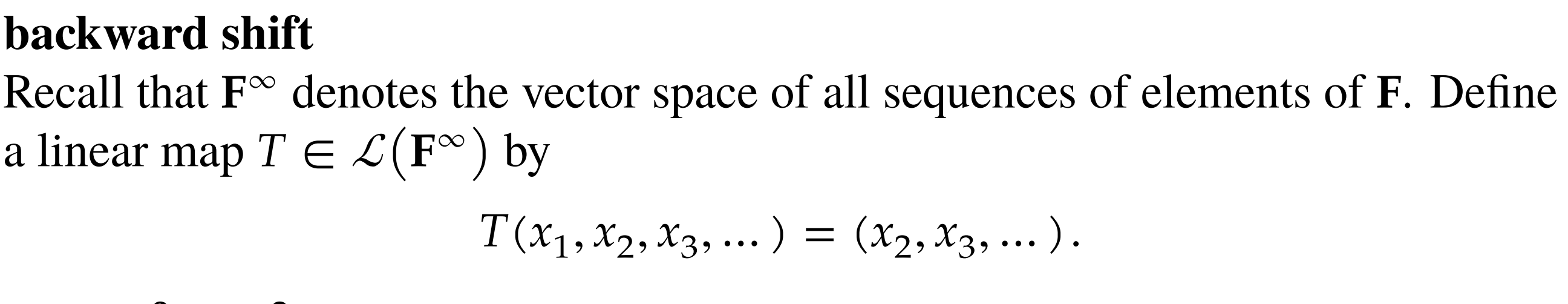
- This is a linear map due to the following proof:
- Addition:
- Let . Then:
- Then
- Homogeneity:
- Let and
- Then, notice:
- Addition:
- This is a linear map due to the following proof:
Linear Map Lemma
Suppose is a basis for and . Then there exists a unique map such that The range here is . Proof:
- Existence
- Consider the map for each
- for each you can take the constant to 1, and the rest to , showing that this is actually a function from to . This makes sense because you can see the constants are shared on both sides
- Proof that T is a linear map
- Addition:
- Let , then:
- Homogenity:
- Let and , Then:
- Addition:
- Uniqueness:
- Lets say there is two functions where and . Then through the properties of additivity and homogeneity these functions must be the same as they take every linear combination to the same linear combination in the range.
Operations on
We can define addition and scaler multiplication on as such: Let and . Then: for
Notice the lambda in the last one is also the same as through homogeneity.
Proof:
- Let
-
- Additivity
- Homogenity
- #todo-week if needed.
- Additivity
is a vector space
With the operations defined above, is a vector space.
Additive identity was defined in an example above.
Multiplication in
Usually we do not multiply vectors because it does not make sense. For this case, however, a useful product exists
Definition of multiplication of linear maps
For we define the product function as: for
todo fix the definition above to show the proper domains. S and T are not in the same set of linear maps, they map different subspaces.
This is similar to composition of functions, think of . Works only when maps to the domain of which makes sense as it needs to be an input.
todo Verify that is indeed a linear map in
Algebraic properties of linear map products
- Associativity then the domains make sense, ( maps to domain of which maps to domain of )
- Identity: for the identity map described before. First is identity operator on V and second is identity operator on W to keep domains consistant.
- Distributive: for and (domains make sense)
Note that Commutativity is missing
todo do a rutine proof to prove the above properties. Idk how much this is needed but could learn smth.
Linear maps / transforms take identity to identity
For and , always maps to
Straight from Abstract Algebra Home
Proof:
- Notice
The above result shows us that, for some function , defined as: Is only a linear map if . This is only the case if , or
Thus linear functions from high school are not the same as linear maps.