2C. Dimension

Length of basis

Any two basis of a finite dimensional vector space have the same length. Proof:

1. Let $b_1$ and $b_2$ be the basis of a vector space $V$.
2. Note that as basis, $b_1$ is a independent list, and $b_2$ is a spanning list, thus $b_1$ can not be of greater length than $b_2$. Prove a similar result in the other direction to show that they have to be of the same size.

Dimension of vector space

The dimension of a vector space $V$ is the length of its basis, denoted by $dimV$

Examples:

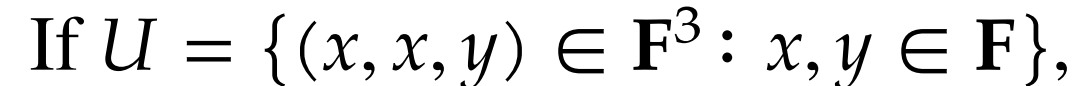Find the following: Dim $F^n$ → $n$ Dim ${\mathcal{P}}_m(z)$ → $m+1$ This entire vector space can be generated with $(1,1,0)(0,0,1)$. These two are also linearly independent, thus they are a basis. The dimension here is $2$

Dimension of a subspace

If $U$ is a subspace of finite vector space $V$, then we have it so $\text{dim}U\le \text{dim}V$ Proof:

1. Let the basis of $U$ be denotes $u_1,u_2,...,u_n$. Then dim $U$ is $n$.
2. Note that $u_1,u_2,...,u_n$ is also an independent list in $V$. By a previous result, this has to be less than the basis of $V$ which is a spanning list. Thus $\text{dim}U\le \text{dim}V$.

Easy proof of basis

Right length definition

Right length + linear independence

Suppose $V$ is a finite dimensional vector space. Then every linearly independent list of length $\text{dim}V$ is a basis of $V$.

Proof:

1. Every linearly independent list can be extended into a basis. However, since the list is the right length, it has to be a basis because every basis is the same length. Thus the extension is just keeping the list as is.

If a subspace shares the same dim, then it is the vector space

Suppose $U$ is a subspace of $V$ and $\text{dim}U=\text{dim}V$. Then we have it so $U=V$

Proof:

1. Assume that $u_1,u_2,...,u_n$ is the basis of $U$. Then this is a linearly independent list in $V$ with length $\text{dim}U=\text{dim}V$. Thus, by the proof above it is also a basis for $V$, causing $U=V$ as $u_1,u_2,...,u_n$ spans both $U$ and $V$

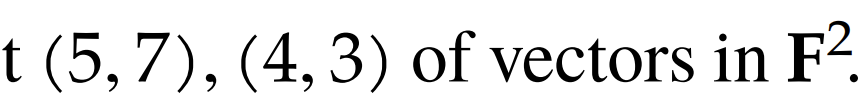We know that $\text{dim}{F}^2=2$. The two vectors are linearly independent as they are not scalar multiples of each other. Thus, is it a basis as its linearly independent of length $\text{dim}{F}^2$.

Right length + spanning list

Suppose $V$ is finite dimensional. Then every spanning list of vectors with length $\text{dim}V$ is a basis of $V$ Proof:

1. Assume $s_1,s_2,...,s_n$ is a spanning list of $V$ of length $\text{dim}V$. Then, as any spanning list can be reduced to a basis, this has to be a basis as no two basis are of different length, so there is nothing to reduce.

Dimension of sum formula

Let $V_1,V_2$ be subspaces of $V$ $\text{dim}(V_1+V_2)=\text{dim}{V}_1+\text{dim}{V}_2-dim(V_1\cap V_2)$

To remember, think of this formula as similar to the union, where the union of a set has as many elements of the first two sets minus their intersection.

todo just memorize this for now and prove later, long proof.

You can make a lot of analoygies to set theory, letting $\#S$ denote the cardinality of $S$. Cardinality is similar to dimension, union is like sum, and disjoint union is like direct sum. Here is a chart to help out: