2A. Span and Linear Independence

Linear algebra focuses on Finite Dimensional Vector Spaces.

Standing assumptions for this chapter:

1. $\mathbb{F}$ denotes either $\mathbb{R}$ or $\mathbb{C}$. We might use $F,R,C$ instead of the bolded version going forward as it is in line with LADR.
2. $V$ denotes a vector space over $F$

List of vectors: Lists of vectors do not need surrounding parenthesis; i.e. For a list of $2$ vectors in $F^3$ we do not use surrounding parenthesis: $(2,6,3),(5,3,7)$ as opposed to $((2,6,3),(5,3,7))$.

Linear Combinations

Definition

The sum of scalar multiples of a list is called the linear combination of a list. Here is an example: Let $v_1,v_2,...,v_n\in V$. Notice these are vectors. Then a linear combination would be $a_1{v}_1+a_2{v}_2+....+a_n{v}_n$ for $a_1,a_2,...,a_n\in F$.

Lets prove that $(17,-4,2)$ is a linear combination of $(2,1,-3),(1,-2,4)$; which is a list of two vectors in ${\mathbb{R}}^3$. Notice: $(17,-4,2)=a_1(2,1,-3)+a_2(1,-2,4)$ For $a_1,a_2\in \mathbb{F}$. This means we have the following set of equations: $2a_1+a_2=17$ $a_1-2a_2=-4$ $-3a_1+4a_2=2$ This is solved by $a_1=6$ and $a_2=5$

Thus $(17,-4,2)$ is a linear combination of $(2,1,-3),(1,-2,4)$.

Similarly, prove if $(17,-4,5)$ is a linear combination of the list of vectors in ${\mathbb{R}}^3$: $(2,1,-3),(1,-2,4)$

Span

Definition

The set of all linear combinations of $v_1,v_2,...,v_n\in V$ is called the span of $v_1,v_2,...,v_n$ denoted $\text{span}(v_1,v_2,...,v_n)$. $\text{span}(v_1,v_2,...,v_n)=\{a_1{v}_1+a_2{v}_2+....+a_n{v}_n\mid a_i\in F\}$ Span of an empty list is defined to be $\{0\}$

Another way to think about it is the span is kind of generated by the base set.

From before, we can see that $(17,-4,2)\in \text{span}((2,1,-3),(1,-2,4))$

Condition

The span of a list of vectors in $V$ is the smallest subspace containing all vectors in that list.

Proof:

1. Lets first prove that the span of a list of vectors is a subspace. Let $U=\text{span}(v_1,v_2,...,v_n)$:
   1. $0\in U$ as $(0,0,....,0)=0v_1+0v_2+...+0v_n$
   2. Additive closure:
      1. Assume that we take two elements in $U$ : $a_1{v}_1+a_2{v}_2+..+a_n{v}_n$ and $b_1{v}_1+b_2{v}_2+..+b_n{v}_n$ for each $a_i,b_i\in \mathbb{F}$
      2. The sum of these elements is as follows: $(a_1{v}_1+a_2{v}_2+..+a_n{v}_n)+(b_1{v}_1+b_2{v}_2+..+b_n{v}_n)=(a_1+b_1)v_1+(a_2+b_2)v_2+....+(a_n+b_n)v_n$
      3. as each $a_i+b_i\in \mathbb{F}$ the sum is also a linear combination of $v_1,v_2,...,v_3$ and therefore is within the span.
   3. Multiplicative closure:
      1. Assume $(a_1{v}_1+a_2{v}_2+..+a_n{v}_n)\in U$ for each $a_i\in \mathbb{F}$ and $\lambda \in \mathbb{F}$.
      2. Then $\lambda (a_1{v}_1+a_2{v}_2+..+a_n{v}_n)=(\lambda a_1{v}_1+\lambda a_2{v}_2+..+\lambda a_n{v}_n)$
      3. As each $\lambda a_i\in \mathbb{F}$ the scalar multiple is also within the span.
2. It is the smallest subspace containing $v_1,v_2,...,v_n$
   1. Assume that we have a subspace containing $v_1,v_2,...,v_n$
   2. For this, first notice that each $v_i\in \text{span}(v_1,v_2,...,v_n)$. This is clear by, for each $v_i$ set $a_i$ to $1$ and the remaining scalars to $0$. This leaves only $v_i$ which is shown as a linear combination of $v_1,v_2,...,v_n$ and therefore part of $\text{span}(v_1,v_2,...,v_n)$
   3. Thus, invoking closure by scalar multiples and addition, all the elements of the span have to be within the set. As each $a_i{v}_i$ is within the set due to scalar multiplicative closure, and then the sum $a_1{v}_1+a_2{v}_2+..+a_n{v}_n$ must also be in the set of all $a_i\in F$.
   4. We have already proves that the span is a subspace, thus as it must contain these elements this must be the smallest subspace.

Notation

If we have it so $V=\text{span}(v_1,v_2,...,v_n)$ we say that $v_1,v_2,...,v_n$ spans $V$

Example

Lets show that $(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)$ spans $F^4$ Proof: We need to show $\text{span}((1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1))=F^4$ $F^4\subset \text{span}((1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1))$:

1. Lets take $x=(x_1,x_2,x_3,x_4)\in F^4$. We can write this as: $(x_1,x_2,x_3,x_4)=x_1(1,0,0,0)+x_2(0,1,0,0)+x_3(0,0,1,0)+x_4(0,0,0,1)$
2. As $x$ can be written as a linear combination of $(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)$, we know that it is within $\text{span}((1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1))$ $\text{span}((1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1))\subset F^4$:
3. Take some element $a\in \text{span}((1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1))$ and let $a=a_1(1,0,0,0)+a_2(0,1,0,0)+a_3(0,0,1,0)+a_4(0,0,0,1)$ for $a_1,a_2,a_3,a_4\in F$.
4. Then notice $a_1(1,0,0,0)+a_2(0,1,0,0)+a_3(0,0,1,0)+a_4(0,0,0,1)=(a_1,a_2,a_3,a_4)\in F^4$
5. Thus any element in the span is an element of $F^4$

Finite dimensional vector space:

Definition

A vector space is called finite dimensional if some list of vectors in it spans the space.

From the example above $F^n$ is a finite vector space.

Polynomials:

Definition:

You already know what they are, but here is more of a formal definition:

1. A function $\mathcal{P}:F\to F$ is called a polynomial if there exists $a_0,a_1,a_2,..,a_n\in F$ such that: $\mathcal{P}(z)=a_0+a_1{x}^1+a_2{x}^2+...+a_n{x}^n$
2. The set of all polynomials with coefficients in $F$ is denoted as $\mathcal{P}(F)$

Prove that $\mathcal{P}(F)$ is a vector space over $(F)$ Proof:

1. Additive properties
   1. Commutative:
      1. Let $a,b\in \mathcal{P}(F)$.
      2. Then let:
         1. $a=a_0+a_1{x}^1+a_2{x}^2+...+a_n{x}^n$
         2. $b=b_0+b_1{x}^1+b_2{x}^2+...+b_n{x}^n$
      3. notice: $a+b=(a_0+a_1{x}^1+a_2{x}^2+...+a_n{x}^n)+(b_0+b_1{x}^1+b_2{x}^2+...+b_n{x}^n)$ $=(a_0+b_0)+(a_1+b_1)x^1+(a_2+b_2)x^2+....+(a_n+b_n)x^n$ $=(b_0+a_0)+(b_1+a_1)x^1+(b_2+a_2)x^2+....+(b_n+a_n)x^n$ $=(b_0+b_1{x}^1+b_2{x}^2+...+b_n{x}^n)+(a_0+a_1{x}^1+a_2{x}^2+...+a_n{x}^n)=b+a$
      4. This additive commutativity is met
   2. Associativity: Proved through a similar process
   3. Identity:
      1. Notice that the 0 function is in $\mathcal{P}(F)$ by setting all the coefficients to $0\in F$.
   4. Inverses:
      1. Let $a=a_0+a_1{x}^1+a_2{x}^2+...+a_n{x}^n\in \mathcal{P}(F)$
      2. $-a=(-a_0)+(-a_1)x^1+(-a_2)x^2+...+(-a_n)x^n\in \mathcal{P}(F)$
      3. Then we have: $a+(-a)=(a_0-a_0)+(a_1-a_1)x^1+(a_2-a_2)x^2+...+(a_n-a_n)x^n=0$
2. Scaler Multiplicative Properties:
   1. Associatively:
      1. Let $\lambda ,\beta \in F$ and $a=a_0+a_1{x}^1+a_2{x}^2+...+a_n{x}^n\in \mathcal{P}(F)$
      2. Then $(\lambda \beta )a=\lambda \beta a_0+\lambda \beta a_1{x}^1+\lambda \beta a_2{x}^2+...+\lambda \beta a_n{x}^n=\lambda (\beta a_0+\beta a_1{x}^1+\beta a_2{x}^2+...+\beta a_n{x}^n)=\lambda (\beta a)$
   2. Identity:
      1. $1$ acts as expected as it just leaves the coefficients as themselves.
3. Distributive Laws:
   1. $\lambda (a+b)=\lambda a+\lambda b$
      1. Trying a summation approach
         1. let $a={\sum }_{i=0}^n{a}_i{x}^i$ and $b={\sum }_{i=0}^n{b}_i{x}^i$.
         2. $\lambda (a+b)=\lambda ({\sum }_{i=0}^n(a_i+b_i)x^i)$
         3. $={\sum }_{i=0}^n(a_i+b_i)\lambda x^i={\sum }_{i=0}^n\lambda a_i{x}^i+{\sum }_{i=0}^n\lambda b_i{x}^i=\lambda a+\lambda b$
   2. $(\alpha +\beta )a=\alpha a+\beta a$
      1. Similar to above
         1. $a={\sum }_{i=0}^n{a}_i{x}^i$
         2. $(\alpha +\beta )a={\sum }_{i=0}^n(\alpha +\beta )a_i{x}^i$
         3. $={\sum }_{i=0}^n\alpha a_i{x}^i+\beta a_i{x}^i$
         4. ${\sum }_{i=0}^n\alpha a_i{x}^i+{\sum }_{i=0}^n\beta a_i{x}^i=\alpha a+\beta a$

Important

If a polynomial is represented by two sets of coefficients, subtracting one representation from the other produces a polynomial that is identically zero as a function on $F$ and hense has all zero coefficients. We will prove this in chapter 4

This means that the coefficients of a polynomial are uniquely determined by the polynomial.

Degree definition

$\text{deg}(p(x))$ is the highest power with a non-zero coefficient. More formally:

if there exists $a_0,a_1,a_2,..,a_n\in F$ such that $a_n\ne 0$ and $\mathcal{P}(x)=a_0+a_1{x}^1+a_2{x}^2+...+a_n{x}^n$ Then this is a polynomial of deg n.

The $0$ polynomial has deg of $-\infty$.

Degree polynomial set notation

${\mathcal{P}}_m(\mathbb{F})$ is the set of all polynomials with at most degree m and coefficients in $\mathbb{F}$.

In the definition above the at most is extremely important, showing that ${\mathcal{P}}_2(\mathbb{F})\subset {\mathcal{P}}_5(\mathbb{F})$

It is easy to see that ${\mathcal{P}}_m(\mathbb{F})=\text{span}(1,x^1,x^2,...,x^k)$. These are elements of ${\mathcal{P}}_m(F)$ because each represents a function in the set, i.e you can get each $x^i$ by setting that specific coeficient to 1 and other ones to 0. And by definition the linear combinations of the functions create ${\mathcal{P}}_m(F)$.

Thus. by this, ${\mathcal{P}}_m(\mathbb{F})$ is a finite dimensional space.

A vector space is called infinite dimensional if it is not finite dimensional, i.e. if there are no list of vectors within the vector space that span the vector space.

$\mathcal{P}(\mathbb{F})$ is finite dimensional

Proof: Take any list of vectors within $\mathcal{P}(\mathbb{F})$, and assume that the largest degree of an element within this list is $m$. Then we can not represent $z^{m+1}$ within this list, thus it can not span all of $\mathcal{P}(\mathbb{F})$.

Linear Independence

Definition

A list of vectors $v_1,v_2,...,v_m\in V$ is called linearly independent if the only way to get $a_1{v}_1+a_2{v}_2+...+a_n{v}_n=0$ is by setting all $a_i=0$. (every coefficient is zero.)

The empty list is declared to be linearly independent.

This is similar to the determination of direct products.

Important Colirary

$v_1,v_2,...,v_m$ is linearly independent $⟺$ each vector in $\text{span}(v_1,v_2,...,v_m)$ has only one representation as a linear combination of $v_1,v_2,...,v_m$. Proof:

1. $v_1,v_2,...,v_m$ is linearly independent $⟹$ each vector in $\text{span}(v_1,v_2,...,v_m)$ has only one representation as a linear combination of $v_1,v_2,...,v_m$.
   1. Assume $v_1,v_2,...,v_m$ is linearly independent, then we have it so that $a_1{v}_1+a_2{v}_2+...+a_n{v}_n=0$ if every $a_i$ is set to $0$.
   2. Now assume, for the sake of contradiction, there are two ways to represent the element $w\in \text{span}(v_1,v_2,...,v_m)$. Then we have it so
      1. $w=x_1{v}_1+x_2{v}_2+...+x_n{v}_n=y_1{v}_1+y_2{v}_2+...+y_n{v}_n$
      2. Now we know subtracting the two gives us $0$; thus: $(x_1{v}_1+x_2{v}_2+...+x_n{v}_n)-(y_1{v}_1+y_2{v}_2+...+y_n{v}_n)=(x_1-y_1)v_1+(x_2-y_2)v_2+...+(x_n-y_n)v_n$
      3. Remember that $v_1,v_2,...,v_m$ is linearly independent. Thus, every coeficent is equal to 0, and for each $x_i-y_i=0$
      4. By this, we have that each $x_i=y_i$ and the two representations are actually the same
2. $v_1,v_2,...,v_m$ is linearly independent $\Leftarrow$ each vector in $\text{span}(v_1,v_2,...,v_m)$ has only one representation as a linear combination of $v_1,v_2,...,v_m$.
   1. Assume each vector in $\text{span}(v_1,v_2,...,v_m)$ has only one representation as a linear combination of $v_1,v_2,...,v_m$.
   2. Setting each coeficent to 0 gives us 0. By definition this can be the only way to represent 0, thus $v_1,v_2,...,v_m$ is linearly independent.

Examples of linear independence:

1. Lets prove $(1,0,0,0),(0,1,0,0),(0,0,1,0)$ are linearly independent in ${\mathbb{R}}^4$
   1. To prove this, we have to show that the only way to get $0$ as a linear combination is by setting all the coefficients to zero.
   2. Notice the following: $a_1(1,0,0,0)+a_2(0,1,0,0)+a_3(0,0,1,0)=(0,0,0,0)$
   3. This means that: $(a_1,0,0,0)+(0,a_2,0,0)+(0,0,a_3,0)=(0,0,0,0)$
   4. The only way for this to happen is $a_1=a_2=a_3=0$. Thus this list is linearly independent.
2. Prove that the list $1,z,...,z^m$ is linearly independent in ${\mathcal{P}}_m(\mathbb{F})$.
   1. The zero function has to move all inputs to zero. This is only possible if: $0_f(z)=0+0z+0z^2+...+0z^n$
   2. Thus this is true. (I let $0_f$ notate the zero function its cooler)
3. A list of length 1 in a vector space is linearly independent $⟺$ it does not contain 0.
   1. Makes sense, as any coefficient scaler multiplied to the 0 vector will equal to 0
   2. The only way for another vector to be equal to 0 is if it is multiplied by the 0 scaler.
4. A list of 2 in a vector space is linearly independent $⟺$ one of the vectors in the list is not a scaler multiple of the other
   1. This makes sense, because if they are a scaler multiple you can create a linear combination with 1 and the multiple amount as the coefficients. I.E $1(6,15)+-3(2,5)=0$

If some vectors are removed from an linearly independent list, the rest of the vectors are still linearly independent

1. This makes sense because if this was not the case the set with the removed vectors would also be included, as they are all just set to zero so they do not really impact the sum outcome.

Linearly dependent definition:

1. A list of vectors is called linearly dependent if it is not linearly independent.
2. In other words, you can write 0 as a linear combination without having all the coefficients equal to 0.

Lets do an example: Prove the following: 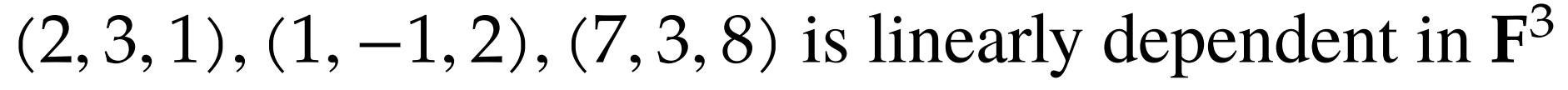#todo after you relearn RREF 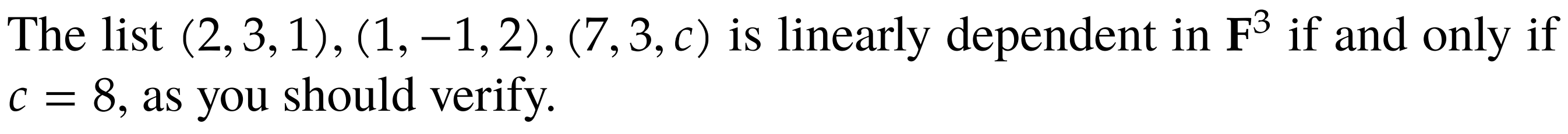#todo similar

Important things to notice

If some vector in the list is a linear combination of other vectors in the list, then the list is linearly dependent. Proof:

1. This clearly holds, as you can just add up the linear combination and set that one vector to -1 in order to get 0.

Every list containing 0 is linearly dependent proof:

1. The coefficient in front of that list can be anything, does not have to be 0, you can still write 0 out as a linear combination.

Linear Dependance Lemma

Suppose $v_1,v_2,...,v_n$ is a linearly dependent list of $V$. Then there exists a $k\in \{1,2,....,n\}$ such that: $v_k\in \text{span}(v_1,v_2,...,v_{k-1})$ Additionally, if $k$ satisfies the condition above and the $k$th term is removed from $v_1,v_2,...,v_n$ then the span of the remaining list equals $\text{span}(v_1,v_2,...,v_n)$. Meaning it does not change the span.

Proof:

1. Proof that $\exists v_k\in \text{span}(v_1,v_2,...,v_{k-1})$.
   1. Let $v_1,v_2,...,v_n$ be a linearly dependent list of $V$. That means there are ways to write $0$ where the coefficients are not zero.
   2. Thus: $a_1{v}_1+a_2{v}_2+....+a_n{v}_n=0$
   3. Let $a_k$ be the largest coefficient which is not zero, i.e you have:
      $a_1{v}_1+a_2{v}_2+....+a_k{v}_k+0+0=0$
   4. Then, you can write $v_k$ as a linear combination of $v_1,v_2,...,v_{k-1}$ $v_k=\frac{a_1}{a_k}{v}_1+\frac{a_2}{a_k}{v}_2+...+\frac{a_{k-1}}{a_k}{v}_{k-1}$
   5. Thus, as it can be written as a linear combination of $v_1,v_2,...,v_{k-1}$, we know $a_k\in \text{span}(v_1,v_2,...,v_{k-1})$
2. Proving the second part of the theorem:
   1. notice that we have it so $v_k=a_1{v}_1+a_2{v}_2+..+a_{k-1}{v}_{k-1}$
   2. Removing $v_k$ does nothing to change the $\text{span}(v_1,v_2,...,v_{k-1})$ as it can still be created by the remaining vectors left on the list. Therefore, we just replace $v_k$ with $a_1{v}_1+a_2{v}_2+..+a_{k-1}{v}_{k-1}$ which works as $a_i\in F$.

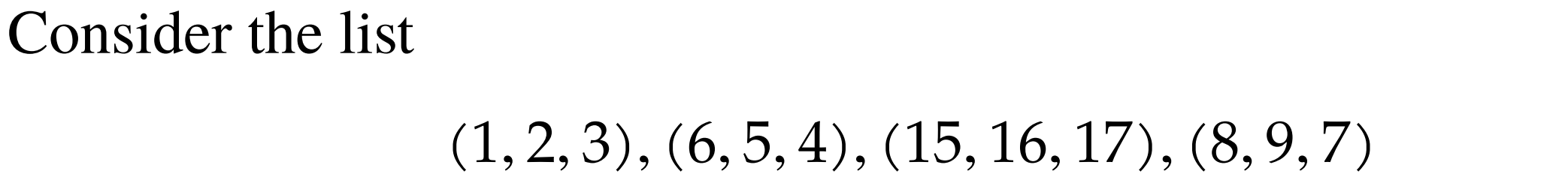#todo for each $v_k$ show if the linear dependance theorem holds. Stop when you find the smallest k for which it holds.

Length of linearly independent list $\le$ length of spanning list

In a finite dimensional vector space V, the length of every linearly independent list of vectors is always greater than or equal to the length of every spanning list of vectors.

Proof:

1. Let $s_1,s_2,...,s_m$ be a spanning list of vectors for $V$ and let $i_1,i_2,...,i_n$ be an independent list for $V$
2. Lets move $i_1$ to the spanning list. The list is now linearly dependent as $i_1\in \text{span}(s_1,s_2,...,s_m)$ due to it being a spanning list. As $i_1\ne 0$ as we defined it to be a part of an independent list and any list with 0 is dependent; there must exist such $s_k$ where $s_k\in \text{span}(i_1,s_1,s_2,...,s_{k-1})$. Remove this $s_k$ so that the spanning list is still of $m$ length, and the span does not change by lemma.
3. Keep doing this with ever $i_k$ in order. you will, by definition, always need an $s_k$ to remove as the list is always linearly dependent, or the list just becomes $i_1,i_2,...,i_n$ which is also a spanning list in that case. Hence the spanning list is either as large as, or larger, than the independent list. $m\ge n$.

Every subspace of a finite dimensional vector space is finite dimensional

Proof:

1. Assume $U$ is a subspace of some finite vector space $V$
2. Now, the next step is repeated. Find some $u_k\in U$ such that $u_k\notin \text{span}(u_1,u_2,...,u_{k-1})$ (The previously picked vectors). Then add it to the list. Stop when there are no such $v_k$ left. As none of the previous vectors span the next ones, the list is linearly independent by the linear independence lemma. And, as all the elements with $U$ are now inside the span, this is a spanning list. Additionally, as this is also an independent list in $V$ it can not be longer than any spanning list of $V$, so it is finite. $■$