Practice Midterm 1

Question 0

0.1

1. Langrange’s theorem states that for any group $G$ and subgroup $H$, the left cosets of $H$ create an equivalence class partitioning $G$. As a byproduct the order of $H$ divides $G$ exactly with the number of cosets known as the index, $[G:H]$. As a formulation: $[G:H]=\frac{\mid G\mid }{\mid H\mid }$

0.2

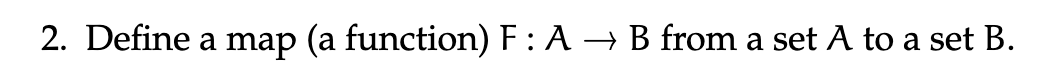
1. A well defined function $F$ would be one where $F(a)=b$, for $a\in A,b\in B$ and each $a$ would only map to one $b$. This relation can be defined as a subset of AxB, where $F(a)=b$ can be shown as $(a,b)$.

0.3

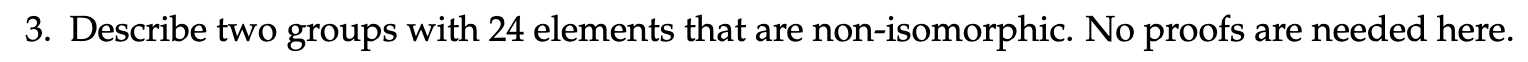
1. $S_4$ has order $4!=24$ and group $Z_{24}$ has order 24. However, $S_4$ is not abelian and $Z_{24}$ is, thus they are not isomorphic.

Problem 1

1.1

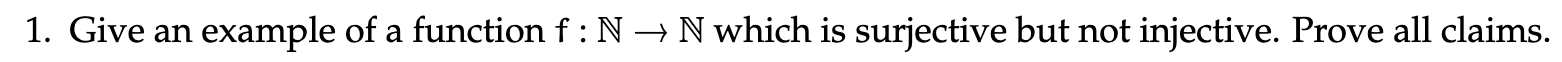
1. Such a function would be f(x)=roof(x/2).
   1. This would clearly get all $N$ in the codomain, but both $1,2$ would map to $1$

1.2

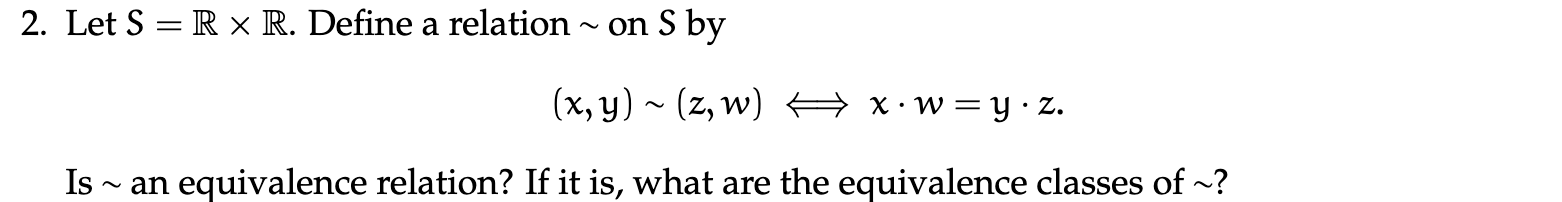
1. lets first check if it is an equivalence relation:
   1. Reflexive:
      1. (x,y)~(x,y):
         1. $x\ast y=y\ast x$ thus this holds
   2. Symmetric:
      1. Assume: (x,y)~(a,b), ie:
         1. $x\ast b=y\ast a$
         2. then, we can see (a,b)~(x,y) as
         3. $a\ast y=b\ast x$
   3. Transitive: 1. Assume (x,y)(a,b), and (a,b)(z,d) 2. Then we know $x\ast b=y\ast aanda\ast d=b\ast z$ 3. From here we want to show (x,y)~(z,d) or $x\ast d=y\ast z$ 4. Multiplying the left equation by d and right equation by y we get $x\ast b\ast d=y\ast a\ast danda\ast d\ast y=b\ast z\ast y$ 5. meaning $x\ast b\ast d=b\ast z\ast y$ 6. or $x\ast d=z\ast y$ which needed to be shown

Problem 2

2.1

1. The order is easily calculated as $LCM(3,5)=15$. Thus ${\tau }^{15}=id$. Then ${\tau }^{13}={\tau }^{-2}$ or:
2. (251)(46783)(251)(46783) = (152)(47368)

2.2

The group $Z_{60}^X$ is the multiplicative group containing call elements relatively prime to 60. This would be $\{1,7,11,13,17,19,23,29,31,37,41,43,47,49,53,59\}$ which has 16 elements. This is a group under multiplication as:

1. Associativity met through definition of binary multiplication in modulo
2. Inverses are met as all elements $m$ s.t. $GCD(m,n)=1$ have inverses in ${\mathbb{Z}}_n$.
3. 1 is the multiplicative identity which is in the group.

2.3

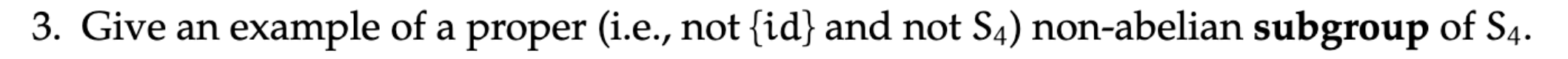$S_3$ is in $S_4$ and is not abelian.

Problem 3

3.1

#review

3.2

G is a group with 19 (prime) elements, thus it is cyclic. This means it can be generated by some element a s.t. $G=⟨a⟩$. If a is e, then we have it so H is also e and both are trivial ($\psi (g)=e_h\forall g\in G$). Suppose a is not 0, then it must be the case that a maps to the generator in h, let $\psi (a)=m$ and for any $g=a^k\in G,\psi (a^k)=\psi (a_1{a}_2...a_k)=\psi (a{)}_1\psi (a{)}_2...\psi (a{)}_k=m^k$ and clearly this is injective as if any two elements map to the same element in $H$ they must be the same power of a in $G$

Because $G$ is a group with prime number of elements, due to langranges theorem its only subgroups are trivial, ie $\{e\}$ or $⟨1⟩$. This means we have only two possible kernels. If the kernel is $\{e\}$ then the homomorphism is injective, if the kernel is the entire ring then the homomorphism is trivial.

review redo, look at possible kernels.

3.3

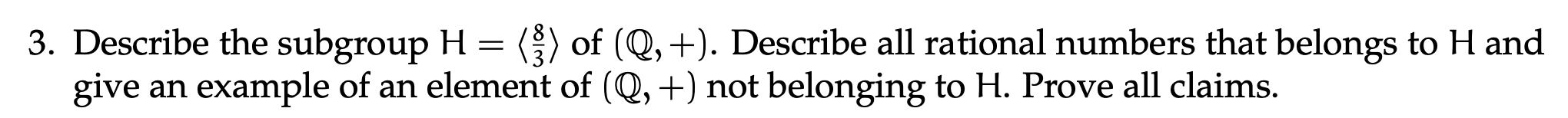$⟨\frac{8}{3}⟩=\{n\frac{8}{3}\mid n\in Z\}$ Clearly, $\frac{7}{3}$ is not in this set.